��Ŀ����
����Ŀ��Ϊ�����п�����������ȡ�úóɼ���ÿλͬѧ������ѵ���������ɼ�Ҳ�����ߣ����Ǵ���Уij��ģ�⿼���������ȡ��50��ͬѧ��һ�������������������Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ������ͼ��ʾ��
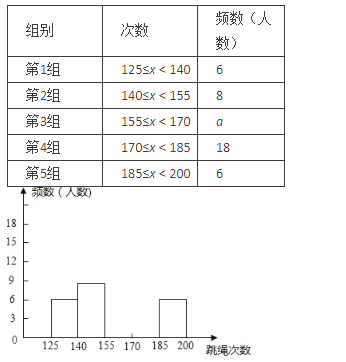
����ͼ������������⣺
��1�����е�a���� ����
��2�����Ƶ���ֲ�ֱ��ͼ����������
��3���������꼶����800��ѧ�����п��忼һ���������������ڵ���185��Ϊ����20�֣�����������Ϣ���������ȫ�꼶ѧ��һ�����������������ֵ�������
���𰸡���1��12����2�������������3��96���ˣ���
��������
��1����������������������֮�ͣ����ɽ�����⣻
��2��3��4��������������ͼ���ɣ�
��3�����������������˼�뼴�ɽ�����⣻
�⣺��1��a��50��6��8��18��6��12���ˣ���
�ʴ�Ϊ12��
��2��Ƶ���ֲ�ֱ��ͼ��ͼ��ʾ��
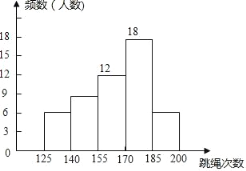
��3�������꼶����800��ѧ���������ֵ�������800��![]() ��96���ˣ���
��96���ˣ���

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ���˶�Ա��С����������һ���Ƕȵķ���������ڲ����ǿ��������������£�С��ķ��и߶�h��m�������ķ���ʱ��t��s��������κ�����ϵ��t��h�ļ����Ӧֵ���±���ʾ��
t��s�� | 0 | 0.5 | 1 | 1.5 | 2 | �� |
h��m�� | 0 | 8.75 | 15 | 18.75 | 20 | �� |
��1����h��t֮��ĺ�����ϵʽ����Ҫ��дt��ȡֵ��Χ����
��2����С�����3sʱ�ĸ߶ȣ�
��3���ʣ�С��ķ��и߶��ܷ�ﵽ22m����˵�����ɣ�

����Ŀ����֪���κ����Ľ���ʽ��y��x2��2x��3��
��1����y��Ľ����������� ���������������� ����
��2��������ϵ��������㷨�����������ߣ�
x | �� | �� | |||||
y | �� | �� |
��3�����ͼ��ش𣺵���2��x��2ʱ������ֵy��ȡֵ��Χ���� ����
����Ŀ��ʡ�����Ϊ�Ӽס��������˶�Ա��ѡ��һ�˲μ�ȫ�������������ǽ��������β��ԣ����Գɼ����±�����λ��������
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | |
�� | 10 | 8 | 9 | 8 | 10 | 9 |
�� | 10 | 7 | 10 | 10 | 9 | 8 |
��1�����ݱ����е����ݣ��������ƽ���ɼ��� �����ҵ�ƽ���ɼ��� ����
��2���ֱ����ס������β��Գɼ��ķ��
��3�����ݣ�1������2������Ľ��������Ϊ�Ƽ�˭�μ�ȫ�����������ʣ���˵�����ɣ�
���㷽��Ĺ�ʽ��s2��![]() [(x1��
[(x1��![]() )2��(x2��
)2��(x2��![]() )2����(xn��
)2����(xn��![]() )2]
)2]