题目内容
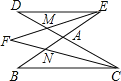
【题目】如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.
(1)求证:OF∥BC;
(2)求证:△AFO≌△CEB;
(3)若EB=5cm,CD=10![]() cm,设OE=x,求x值及阴影部分的面积.
cm,设OE=x,求x值及阴影部分的面积.

【答案】(1)证明见解析;(2)证明见解析;(3)阴影部分的面积是:(![]() ﹣25
﹣25![]() )cm2.
)cm2.
【解析】
(1)根据直径所对的圆周角是直角,以及垂直于同一直线的两直线平行即可证得;
(2)根据垂径定理以及等弧所对的圆周角相等,即可证得:△AFO和△CEB的两个角相等,从而证得两个三角形相似;
(3)根据勾股定理求得x的值,然后根据阴影部分的面积=扇形COD的面积-△COD的面积即可求解.
(1)∵AB为⊙O的直径,
∴AC⊥BC
又∵OF⊥AC
∴OF∥BC
(2)∵AB⊥CD
∴![]() =
=![]() ,
,
∴∠CAB=∠BCD
又∵∠AFO=∠CEB=90°,OF=BE,
∴△AFO≌△CEB
(3)连接DO.设OE=x,
∵AB⊥CD
∴![]()
在△OCB中,OC=OB=x+5(cm),
根据勾股定理可得:![]()
解得:x=5,即OE=5cm,
∴![]()
∴∠COE=60°
∴∠COD=120°,
∴扇形COD的面积是: ![]()
△COD的面积是:![]()
∴阴影部分的面积是: ![]() cm2.
cm2.

练习册系列答案
相关题目
【题目】本学期学校开展以“感受中华传统美德”为主题的研学活动,组织150名学生参观历史博物馆和民俗展览馆,每一名学生只能参加其中一项活动,共支付票款2000元,票价信息如下:
地点 | 票价 |
历史博物馆 | 10元/人 |
民俗展览馆 | 20元/人 |
(1)请问参观历史博物馆和民俗展览馆的人数各是多少人?
(2)若学生都去参观历史博物馆,则能节省票款多少元?