��Ŀ����
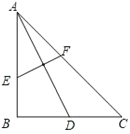
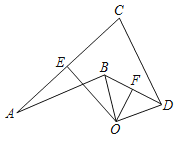
����Ŀ����ABC��һ�ŵ���ֱ��������ֽ�壬��C=Rt����AC=BC=2��Ҫ������ֽ���м���һ�������ܴ�������Σ�������ͼ1��ʾ����ͼ1�м�����Ϊ��1�μ�ȡ�������õ����������ΪS1������ͼ1�еļ����������µ���ADE����BDF�У��ֱ��ȡ�����Σ��õ�������ͬ�������Σ���Ϊ��2�μ�ȡ�����������������������ΪS2����ͼ2������S2=_____���������µ��ĸ��������У���ͬ���ķ����ֱ��ȡ�����Σ��õ��ĸ���ͬ�������Σ���Ϊ��3�μ�ȡ���������ĸ������ε������ΪS3����ͼ3��������������ȥ�����2018�μ�ȡ��S2018=_____��

���𰸡�![]()
![]()
��������
�������⣬�����![]() ,ͬ���ɵù���Sn���ǵ�n�μ�ȡ��ʣ������������ͣ����ݴ˹�����⼴�ɵô�.
,ͬ���ɵù���Sn���ǵ�n�μ�ȡ��ʣ������������ͣ����ݴ˹�����⼴�ɵô�.
���ı���ECFDΪ�����Σ���ED��EC��CF��DF,��AED����DFB��90�㣬�ߡ�ABC�ǵ���ֱ�������Σ����A����B��45�㣬��AE��DE��CE��DF��BF��EC��CF,��AC��BC��2����DE��DF��1����S��AED��S��BDF��S������ECDF��1;ͬ��S2���ǵڶ��μ�ȡ���ʣ�������ε�����ͣ�Sn��Ϊ��n�μ�ȡ�������������ͣ����һ�μ�ȡ��ʣ�������ε������Ϊ2��S1��1��S1,�ڶ��μ�ȡ��ʣ�������ε������ΪS1��S2��![]() ��S2�������μ�ȡ��ʣ�������ε������ΪS2��S3��
��S2�������μ�ȡ��ʣ�������ε������ΪS2��S3��![]() ��S3�����2018�μ�ȡ��ʣ�������ε������ΪS2017��S2018��
��S3�����2018�μ�ȡ��ʣ�������ε������ΪS2017��S2018��![]() .
.