题目内容
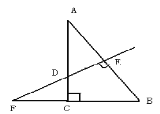
【题目】如图,已知Rt△ABC中,∠ACB=90°,∠B=15°,边AB的垂直平分线交边BC于点E,垂足为点D,取线段BE的中点F,联结DF.求证:AC=DF.(说明:此题的证明过程需要批注理由)

【答案】见解析
【解析】
先根据线段垂直平分线的性质得:AE=BE,再利用直角三角形斜边中线的性质得:DF与BE的关系,最后根据直角三角形30度的性质得AC和AE的关系,从而得出结论.
连接AE,
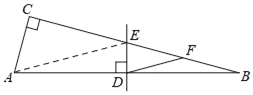
∵DE是AB的垂直平分线(已知),
∴AE=BE,∠EDB=90°(线段垂直平分线的性质),
∴∠EAB=∠EBA=15°(等边对等角),
∴∠AEC=30°(三角形的一个外角等于与它不相邻的两个内角的和),
Rt△EDB中,∵F是BE的中点(已知),
∴DF=![]() BE(直角三角形斜边中线等于斜边的一半),
BE(直角三角形斜边中线等于斜边的一半),
Rt△ACE中,∵∠AEC=30°(已知),
∴AC=![]() AE(直角三角形30°角所对的直角边是斜边的一半),
AE(直角三角形30°角所对的直角边是斜边的一半),
∴AC=DF(等量代换).

练习册系列答案
相关题目