题目内容
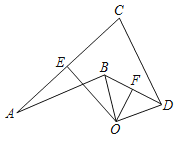
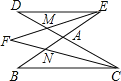
【题目】如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线,EF与CD交于点M,CF与BE交于点N.
(1)若∠D=70°,∠BED=30°,则∠EMA= (度);
(2)若∠B=60°,∠BCD=40°,则∠ENC= (度);
(3)∠F与∠B、∠D有怎样的数量关系?证明你的结论.
【答案】(1)85;(2)80;(3)∠F=![]() (∠B+∠D).
(∠B+∠D).
【解析】
(1)利用角平分线的性质以及三角形外角的性质求解即可;
(2)利用角平分线的性质以及三角形外角的性质求解即可;
(3)利用三角形外角的性质求得∠D+∠DEF+∠B+∠BCF=∠F+∠DCF+∠F+∠BEF,利用角平分线的性质可证得∠B+∠D=2∠F,从而求得答案.
(1)∵EF为∠BED的平分线,∠BED=30°,
∴∠DEM=∠FEN=![]() ∠BED=15°.
∠BED=15°.
又∵∠EMA=∠D+∠DEM,∠D=70°,
∴∠EMA=85°.
故答案为:85°.
(2)∵CF为∠BCD的平分线,∠BCD=40°,
∴∠BCN=∠FCM=![]() ∠BCD=20°.
∠BCD=20°.
又∵∠ENC=∠B+∠BCN,∠B=60°,
∴∠ENC=80°.
故答案为:80°.
(3)∠F=![]() (∠B+∠D).
(∠B+∠D).
证明:∵∠EMA=∠D+∠DEF=∠F+∠DCF,
∠ENC=∠B+∠BCF=∠F+∠BEF,
∴∠D+∠DEF+∠B+∠BCF=∠F+∠DCF+∠F+∠BEF.
又∵CF为∠BCD的平分线,EF为∠BED的平分线,
∴∠DEF=∠BEF,∠DCF=∠BCF.
∴∠B+∠D=2∠F.
即:∠F=![]() (∠B+∠D).
(∠B+∠D).

练习册系列答案
相关题目