题目内容
【题目】直线AB:y=-x-b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.

(1)求点B的坐标;
(2)求直线BC的解析式;
(3)直线EF:y=2x-k(k≠0)交AB于E,交BC于点F,交x轴于点D,是否存在这样的直线EF,使得S△EBD=S△FBD?若存在,求出k的值;若不存在,请说明理由.
【答案】(1) B点坐标为:(0,6).(2) y=3x+6.(3) k=-2.4
【解析】
试题(1)将点A(6,0)代入直线AB的解析式,可得b的值,继而可得点B的坐标;
(2)设BC的解析式是y=ax+c,根据B点的坐标,求出C点坐标,把B,C点的坐标分别代入求出a和c的值即可;
(3)过E、F分别作EM⊥x轴,FN⊥x轴,则∠EMD=∠FND=90°,有题目的条件证明△NFD≌△EDM,进而得到FN=ME,联立直线AB:y=-x-b和y=2x-k求出交点E和F的纵坐标,再利用等底等高的三角形面积相等即可求出k的值;
试题解析:(1)将点A(6,0)代入直线AB解析式可得:0=-6-b,
解得:b=-6,
∴直线AB 解析式为y=-x+6,
∴B点坐标为:(0,6).
(2)∵OB:OC=3:1,
∴OC=2,
∴点C的坐标为(-2,0),
设BC的解析式是y=ax+c,代入得;![]() ,
,
解得:![]() ,
,
∴直线BC的解析式是:y=3x+6.
(3)过E、F分别作EM⊥x轴,FN⊥x轴,则∠EMD=∠FND=90°.
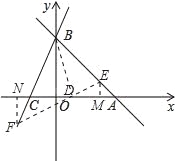
∵S△EBD=S△FBD,
∴DE=DF.
又∵∠NDF=∠EDM,
∴△NFD≌△EDM,
∴FN=ME,
联立得![]() ,
,
解得:yE=-![]() k+4,
k+4,
联立![]() ,
,
解得:yF=-3k-12,
∵FN=-yF,ME=yE,
∴3k+12=-![]() k+4,
k+4,
∴k=-2.4;
当k=-2.4时,存在直线EF:y=2x-2.4,使得S△EBD=S△FBD.

【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | | 8 | 0.4 |
乙 | | 9 | | 3.2 |
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).