Question

【题目】平面内的两条直线有相交和平行两种位置关系．

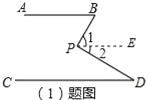
（1）如图1，若AB∥CD，点P在AB、CD内部，∠B=50°，∠D=30°，求∠BPD．

（2）如图2，将点P移到AB、CD外部，则∠BPD、∠B、∠D之间有何数量关系？（不需证明）

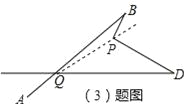
（3）如图3，写出∠BPD﹑∠B﹑∠D﹑∠BQD之间的数量关系？请证明你的结论．

（4）如图4，求出∠A+∠B+∠C+∠D+∠E+∠F的度数．

Answer 1

【答案】（1）80°；（2）∠B=∠BPD+∠D，证明见解析；（3）∠BPD=∠BQD+∠B+∠D；（4）360°

【解答】

【解析】试题（1）过点P作PE∥AB，根据两直线平行，内错角相等可得∠B=∠1，∠D=∠2，再根据∠BPD=∠1+∠2代入数据计算即可得解；（2）根据根据两直线平行，内错角相等可得∠BOD=∠B，然后根据三角形的一个外角等于与它不相邻的两个内角的和列式整理即可得解；（3）连接QP并延长，再根据三角形的一个外角等于与它不相邻的两个内角的和解答；（4）根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠E=∠1，∠B+∠F=∠2，再根据四边形的内角和定理列式计算即可得解．

试题解析：

解：（1）过点P作PE∥AB，

∵AB∥CD，

∴AB∥EP∥CD，

∴∠B=∠1=50°，∠D=∠2=30°，

∴∠BPD=80°；

（2）∠B=∠BPD+∠D．

（3）如图，连接QP并延长，

结论：∠BPD=∠BQD+∠B+∠D．

理由：略

（4）如图，由三角形的外角性质，∠A+∠E=∠1，∠B+∠F=∠2，

∵∠1+∠2+∠C+∠D=360°，

∴∠A+∠B+∠C+∠D+∠E+∠F=360°．

点晴：本题考查了平行线的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记性质并作出辅助线是解题的关键．