题目内容
【题目】问题提出:
某校要举办足球赛,若有5支球队进行单循环比赛(即全部比赛过程中任何一队都要分别与其他各队比赛一场且只比赛一场),则该校一共要安排多少场比赛?
构建模型:
生活中的许多实际问题,往往需要构建相应的数学模型,利用模型的思想来解决问题.
为解决上述问题,我们构建如下数学模型:
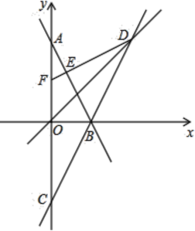
(1)如图①,我们可以在平面内画出5个点(任意3个点都不在同一条直线上),其中每个点各代表一支足球队,两支球队之间比赛一场就用一条线段把他们连接起来.由于每支球队都要与其他各队比赛一场,即每个点与另外4个点都可连成一条线段,这样一共连成5×4条线段,而每两个点之间的线段都重复计算了一次,实际只有 条线段,所以该校一共要安排 场比赛.

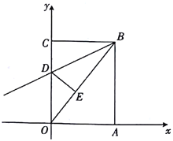
(2)若学校有6支足球队进行单循环比赛,借助图②,我们可知该校一共要安排__________场比赛;
…………
(3)根据以上规律,若学校有n支足球队进行单循环比赛,则该校一共要安排___________场比赛.
实际应用:
(4)9月1日开学时,老师为了让全班新同学互相认识,请班上42位新同学每两个人都相互握一次手,全班同学总共握手________________次.
拓展提高:
(5)往返于青岛和济南的同一辆高速列车,中途经青岛北站、潍坊、青州、淄博4个车站(每种车票票面都印有上车站名称与下车站名称),那么在这段线路上往返行车,要准备车票的种数为__________种.
【答案】(1)10,10;(2)15;(3)![]() ;(4)861;(5)30
;(4)861;(5)30
【解析】
(1)根据图①线段数量进行作答.
(2)根据图②线段数量进行作答.
(3)根据每个点存在n-1条与其他点的连线,而每两个点之间的线段都重复计算了一次,提出假设,当![]() 时均成立,假设成立.
时均成立,假设成立.
(4)根据题意,代入![]() 求解即可.
求解即可.
(5)根据题意,代入![]() 求解即可.
求解即可.
(1)由图①可知,图中共有10条线段,所以该校一共要安排10场比赛.
(2)由图②可知,图中共有15条线段,所以该校一共要安排15场比赛.
(3)根据图①和图②可知,若学校有n支足球队进行单循环比赛,则每个点存在n-1条与其他点的连线,而每两个点之间的线段都重复计算了一次
∴若学校有n支足球队进行单循环比赛,则该校一共要安排![]() 场比赛.
场比赛.
当![]() 时均成立,所以假设成立.
时均成立,所以假设成立.
(4)将n=42代入关系式中
![]()
∴全班同学总共握手861次.
(5)因为行车往返存在方向性,所以不需要除去每两个点之间的线段都重复计算了一次的情况
将n=6代入![]() 中
中
解得![]()
∴要准备车票的种数为30种.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案