题目内容
【题目】如图,在△ABC中,动点P在∠ABC的平分线BD上,动点M在BC边上,若BC=3,∠ABC=45°,则PM+PC的最小值是( )

A. 2 B. ![]() C.
C. ![]() D. 3
D. 3
【答案】B
【解析】分析:截取BE=BM,所以△BEP≌△BMP(SAS),根据点到直线的距离垂线段最短可知CE⊥AB,根据解直角三角形即可求解.
详解:如图:
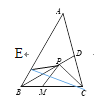
在AB上截取BE=BN,在△BEP和△BMP中,
 ,
,
∴△BEP≌△BMP(SAS),
∴MP=EP.
连接CE,
即:CE![]() PE+PC
PE+PC
当CE![]() PE+PC
PE+PC
即:CE与BP的交点即为点P,
当CE⊥AB时,CE最短(点到直线的距离垂线段最短).
∵∠ABC=45°,
∴∠EBC=∠BCE=45°.
∴sin∠EBC=![]() ,且BC=3,
,且BC=3,
∴EC=![]() .
.

练习册系列答案
相关题目
【题目】某旅行社拟在暑假期间面向学生推出“林州红旗渠一日游”活动,收费标准如下:
人数m | 0<m≤100 | 100<m≤200 | m>200 |
收费标准(元/人) | 90 | 85 | 75 |
甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于100人,乙校报名参加的学生人数少于100人.经核算,若两校分别组团共需花费20 800元,若两校联合组团只需花费18 000元.
(1)两所学校报名参加旅游的学生人数之和超过200人吗?为什么?
(2)两所学校报名参加旅游的学生各有多少人?