题目内容
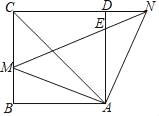
【题目】小明遇到这样一个问题,如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC.求∠C的度数。小明通过探究发现,延长CD至点Q,使BQ=AB,再证明△ADC≌△ADQ,使问题得到解决.

(1)根据阅读材料回答,△ADC≌△ADQ的条件是________(填SSS,SAS,AAS,ASA,或HL)
(2)参考小明思考问题的方法,解答下列问题:求∠C的度数;
(3)解决问题,如图,已知,△ABC中,过点B任意作射线l,在l上取一点D,使∠ABD=∠ACD,AM⊥BD于点M,且BM=MD+CD。探究AB与AC的数量关系,并证明.

【答案】(1)证明见解析;(2)∠C=20°;(3)AB=AC,理由见解析.
【解析】
(1)根据SAS即可证明;
(2)根据△ADQ≌△ADC,推出∠ABC=2∠Q=2∠C,即可解决问题;
(3)如图,在MB上截取MH=DM,连接AH、AD,作HF⊥AB于F,作DE⊥AC于E,先证明△BHF≌△CDE,推出HF=DE,由AH=AD,推出Rt△AHF≌Rt△ADE,推出∠BAH=∠CAD,由∠ABH=∠ACD,BH=CD,再证明△ABH≌△ACD即可解决问题.
(1)如图,延长CD至点Q,使BQ=AB,

∵AD⊥BC于D,
∴∠ADC=∠ADQ=90°,
∵AB+BD=CD,AB=BQ,
∴BD+BQ=DQ=DC,
∵AD=AD,
∴△ADQ≌△ADC(SAS),
∴△ADC≌△ADQ的理由是(SAS);
(2)∵△ADQ≌△ADC
∴∠Q=∠C,
∵BA=BQ,
∴∠Q=∠BAQ,
∵∠ABC=∠Q+∠BAQ,
∴∠ABC=2∠C,
∵∠BAC=120°,
∴3∠C=60°,
∴∠C=20°;
(3)AB=AC,
理由:如图,在MB上截取MH=DM,连接AH、AD.作HF⊥AB于F,作DE⊥AC于E.

∵AM⊥DH,MH=MD,
∴AH=AD,
∵BM=DM+DC=BH+MH,
∵CD=BH,
∵∠DEC=∠HFB=90°,∠HBF=∠DCE,
∴△BHF≌△CDE,
∴HF=DE,
∵AH=AD,
∴Rt△AHF≌Rt△ADE,
∴∠BAH=∠CAD,
∵∠ABH=∠ACD,BH=CD,
∴△ABH≌△ACD,
∴AB=AC.