Ő‚ńŅńŕ»›
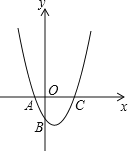
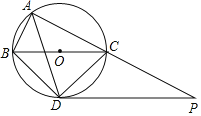
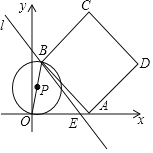
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨“—÷™÷ĪŌŖl£ļy£Ĺ©Ā![]() x+8ĹĽx÷Š”ŕĶ„E£¨Ķ„Aő™x÷Š…ŌĶń“ĽłŲ∂ĮĶ„£®Ķ„A≤Ľ”ŽĶ„E÷ōļŌ£©£¨‘ŕ÷ĪŌŖl…Ō»°“ĽĶ„B£®Ķ„B‘ŕx÷Š…Ō∑Ĺ£©£¨ ĻBE£Ĺ5AE£¨Ń¨ĹŠAB£¨“‘ABő™ĪŖ‘ŕABĶń”“≤ŗ◊ų’ż∑Ĺ–őABCD£¨Ń¨ĹŠOB£¨“‘OBő™÷Īĺ∂◊ų°—P£ģ
x+8ĹĽx÷Š”ŕĶ„E£¨Ķ„Aő™x÷Š…ŌĶń“ĽłŲ∂ĮĶ„£®Ķ„A≤Ľ”ŽĶ„E÷ōļŌ£©£¨‘ŕ÷ĪŌŖl…Ō»°“ĽĶ„B£®Ķ„B‘ŕx÷Š…Ō∑Ĺ£©£¨ ĻBE£Ĺ5AE£¨Ń¨ĹŠAB£¨“‘ABő™ĪŖ‘ŕABĶń”“≤ŗ◊ų’ż∑Ĺ–őABCD£¨Ń¨ĹŠOB£¨“‘OBő™÷Īĺ∂◊ų°—P£ģ
£®1£©ĶĪĶ„A‘ŕĶ„E◊ů≤ŗ Ī£¨»ŰĶ„B¬š‘ŕy÷Š…Ō£¨‘ÚAEĶń≥§ő™°° °°£¨Ķ„DĶń◊ÝĪÍő™°° °°£Ľ
£®2£©»Ű°—P”Ž’ż∑Ĺ–őABCDĶńĪŖŌŗ«–”ŕĶ„B£¨«ůĶ„BĶń◊ÝĪÍ£Ľ
£®3£©°—P”Ž÷ĪŌŖBEĶńĹĽĶ„ő™Q£¨Ń¨ĹŠCQ£¨ĶĪCQ∆Ĺ∑÷°ŌBCD Ī£¨BEĶń≥§ő™°° °°£ģ£®÷ĪĹ”–ī≥Ųīūįł£©
°ĺīūįł°Ņ£®1£©2£¨£®12£¨4£©£Ľ£®2£©¬ķ◊„ŐűľĢĶńĶ„BĶń◊ÝĪÍő™£®©Ā12£¨24£©ĽÚ£®![]() £¨
£¨![]() £©ĽÚ£®
£©ĽÚ£®![]() £¨
£¨![]() £©£Ľ£®3£©
£©£Ľ£®3£©![]() £ģ
£ģ
°ĺĹ‚őŲ°Ņ
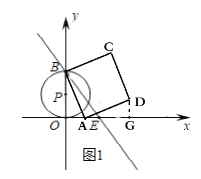
£®1£©»ÁÕľ1÷–£¨◊ųDG°Õx÷Š”ŕG£ģÕ®Ļż÷§√ų°ųOBA°’°ųDAGľīŅ…Ķ√≥ŲĶ„DĶń◊ÝĪÍ£Ľ
£®2£©∑÷»ż÷÷÷÷«ť–ő£ļ»ÁÕľ2÷–£¨ĶĪĶ„A”Ž‘≠Ķ„O÷ōļŌ Ī£¨°—P”ŽBCŌŗ«–”ŕĶ„B£¨AE£Ĺ6£¨»ÁÕľ4÷–£¨ĶĪOB°ÕAB Ī£¨°—P”ŽABŌŗ«–”ŕĶ„B£¨◊ųBH°ÕOA”ŕH£ģ∑÷Īū«ůĹ‚ľīŅ…£¨»ÁÕľ4÷–£¨ĶĪĶ„E‘ŕĶ„AĶń”“≤ŗ Ī£¨◊ųBH°ÕOA”ŕH£ģņŻ”√Ōŗň∆»żĹ«–őĶń–‘÷ «ůĹ‚ľīŅ…£Ľ
£®3£©»ÁÕľ5£¨◊ųBG°ÕOA”ŕĶ„G£¨Ń¨ĹŠOQ£ģ…ŤAE£Ĺm£¨‘ÚBE£Ĺ5m£¨Ķ√ĶĹBG£Ĺ4m£¨EG£Ĺ3m£¨AG£Ĺ2m£¨«ůĶ√B£®6©Ā3m£¨4m£©£¨C£®m+6£¨6m£©£¨A£®6©Ām£¨0£©£¨Ķ√ĶĹ÷ĪŌŖOQĶńĹ‚őŲ Ĺő™![]() £¨«ůĶ√
£¨«ůĶ√![]() £¨Õ∆≥ŲC£¨Q£¨A»żĶ„Ļ≤ŌŖ£¨Ĺ‚∑Ĺ≥ŐľīŅ…Ķ√ĶĹĹŠ¬Ř£ģ
£¨Õ∆≥ŲC£¨Q£¨A»żĶ„Ļ≤ŌŖ£¨Ĺ‚∑Ĺ≥ŐľīŅ…Ķ√ĶĹĹŠ¬Ř£ģ
Ĺ‚£ļ£®1£©»ÁÕľ1÷–£¨◊ųDG°Õx÷Š”ŕG£ģ
”…Ő‚“‚£ļE£®6£¨0£©£¨B£®0£¨8£©£¨
°ŗOE£Ĺ6£¨OB£Ĺ8£¨
°ŗBE£Ĺ![]() £Ĺ10£¨
£Ĺ10£¨
°ŖBE£Ĺ5AE£¨
°ŗAE£Ĺ2£¨
°ŗOA£Ĺ4£¨
°Ŗ°ŌOBA+°ŌOAB=°ŌOAB+°ŌDAG=90,
°ŗ°ŌBAO£Ĺ°ŌDAG£¨
°ŖAB=DA£¨°ŌAOB£Ĺ°ŌDGA,
°ŗ°ųOBA°’°ųDAG(AAS)£¨
°ŗDG=OA=4,OB=AG=8£¨
°ŗOG=OA+AG=12,
°ŗD£®12£¨4£©£¨
Ļ īūįłő™2£¨£®12£¨4£©£Ľ
£®2£©»ÁÕľ2÷–£¨ĶĪĶ„A”Ž‘≠Ķ„O÷ōļŌ Ī£¨°—P”ŽBCŌŗ«–”ŕĶ„B£¨AE£Ĺ6£¨
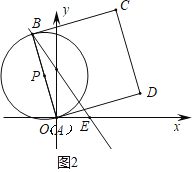
°ŖBE£Ĺ5AE£¨
°ŗBE£Ĺ30£¨Ņ…Ķ√B£®©Ā12£¨24£©£ģ
»ÁÕľ3÷–£¨ĶĪOB°ÕAB Ī£¨°—P”ŽABŌŗ«–”ŕĶ„B£¨◊ųBH°ÕOA”ŕH£ģ
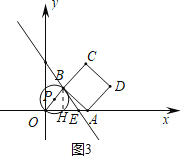
…ŤAE£Ĺm£¨‘ÚBE£Ĺ5m£¨BH£Ĺ4m£¨EH£Ĺ3m£¨
°ŗBH£ĹAH£Ĺ4m£¨
°ŗ°ŌBAO£Ĺ45°„£¨
°Ŗ°ŌOBA£Ĺ90°„£¨
°ŗ°ŌBOA£Ĺ45°„£¨
°ŗĶ„BĶńļŠ◊ÝĪÍ”Ž◊›◊ÝĪÍŌŗÕ¨£¨Ņ…Ķ√B£®![]() £¨
£¨![]() £©£¨
£©£¨
»ÁÕľ4÷–£¨ĶĪĶ„E‘ŕĶ„AĶń”“≤ŗ Ī£¨◊ųBH°ÕOA”ŕH£ģ
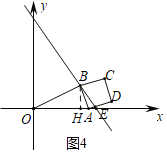
…ŤBE£Ĺ5m£¨AE£Ĺm£¨‘ÚBH£Ĺ4m£¨AEH£Ĺ3m£¨AH£Ĺ2m£¨
°Ŗ°ŌOBA£Ĺ°ŌOHB£Ĺ90°„£¨
”…°ųOHB°◊°ųBHA£¨Ņ…Ķ√BH2£ĹOHAH£¨
°ŗ16m2£Ĺ£®6©Ā3m£©2m£¨
Ĺ‚Ķ√m£Ĺ![]() £¨
£¨
°ŗB£®![]() £¨
£¨![]() £©
£©
◊Ř…Ōňý Ų£¨¬ķ◊„ŐűľĢĶńĶ„BĶń◊ÝĪÍő™£®©Ā12£¨24£©ĽÚ£®![]() £¨
£¨![]() £©ĽÚ£®
£©ĽÚ£®![]() £¨
£¨![]() £©£Ľ
£©£Ľ
£®3£©»ÁÕľ5£¨◊ųBG°ÕOA”ŕĶ„G£¨Ń¨ĹŠOQ£ģ
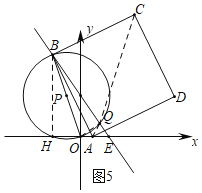
…ŤAE£Ĺm£¨‘ÚBE£Ĺ5m£¨
°ŗBG£Ĺ4m£¨EG£Ĺ3m£¨AG£Ĺ2m£¨
°ŗB£®6©Ā3m£¨4m£©£¨C£®m+6£¨6m£©£¨A£®6©Ām£¨0£©£¨
°ŖOQ°Õ÷ĪŌŖl£¨«“Ļż‘≤–ńO£¨
°ŗ÷ĪŌŖOQĶńĹ‚őŲ Ĺő™![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŖCQ∆Ĺ∑÷°ŌBCD£¨
°ŗC£¨Q£¨A»żĶ„Ļ≤ŌŖ£¨
°ŗ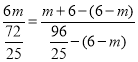 £¨
£¨
Ĺ‚Ķ√![]() £¨
£¨
°ŗ![]() £¨
£¨
span>°ŗ![]() £¨
£¨
Ļ īūįłő™£ļ![]() £ģ
£ģ

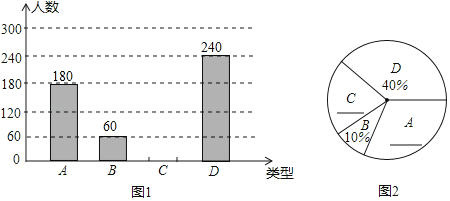
°ĺŐ‚ńŅ°Ņń≥«ÝĹŐŅ∆‘ļŌŽŃňĹ‚ł√«Ý÷–Ņľ ż—ß ‘Ő‚÷–Õ≥ľ∆Ő‚ĶńĶ√∑÷«ťŅŲ£¨ī”ľ◊°Ę““ŃĹňý—ß–£łųňśĽķ≥ť»°Ńň20√Ż—ß…ķĶń—ß…ķ≥…ľ®»ÁŌ¬£ģ£®ł√Ő‚¬ķ∑÷10∑÷£¨—ß…ķĶ√∑÷ĺýő™’Ż ż£©ľ◊—ß–£20√Ż—ß…ķ≥…ľ®£®Ķ•őĽ£ļ∑÷£©∑÷Īūő™£ļ7£¨7£¨8£¨9£¨8£¨6£¨7£¨8£¨8£¨10£¨7£¨9£¨6£¨8£¨7£¨8£¨9£¨7£¨8£¨9£ģ““—ß–£20√Ż—ß…ķ—ß…ķ≥…ľ®ĶńŐű–őÕ≥ľ∆Õľ»ÁÕľňý ĺ£ļ
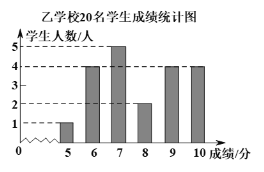
ĺ≠Ļż∂‘ŃĹ–£’‚20√Ż—ß…ķ≥…ľ®Ķń’ŻņŪ£¨Ķ√ĶĹ∑÷őŲ żĺ›»ÁŌ¬ĪŪ£ļ
◊ťĪū | ľę≤Ó | ∆Ĺĺý∑÷ | ÷–őĽ ż | ∑Ĺ≤Ó |
ľ◊ | 4 | b | 8 | 1£ģ05 |
““ | a | 7£ģ8 | c | 2£ģ46 |
£®1£©«ů≥ŲĪŪ÷–Ķńa°Ęb°ĘcĶń÷Ķ£ģ
£®2£©ł√Ő‚Ķ√∑÷8∑÷ľį∆š“‘…Ōľīő™”Ň–„£¨“—÷™ľ◊—ß–£”–1200»ň£¨«ŽĻņň„ľ◊—ß–£Ķń”Ň–„»ň ż”–∂ŗ…Ŕ»ň£Ņ
£®3£©«Žń„ĹŠļŌ“‘…Ō∑÷őŲ żĺ›ňĶ√ų ‘Ő‚÷–Õ≥ľ∆Ő‚Ķ√∑÷”Ň–„ĶńņŪ”…£ģ