Question

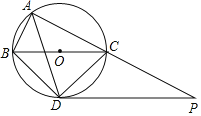
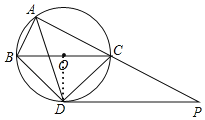
【题目】如图，⊙O是△ABC的外接圆，点O在BC边上，∠BAC的平分线交⊙O于点D，连接BD、CD，过点D作BC的平行线与AC的延长线相交于点P．

（1）求证：PD是⊙O的切线；

（2）求证：△ABD∽△DCP；

（3）当AB=5cm，AC=12cm时，求线段PC的长．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）CP=16.9cm．

【解析】（1）先判断出∠BAC=2∠BAD，进而判断出∠BOD=∠BAC=90°，得出PD⊥OD即可得出结论；

（2）先判断出∠ADB=∠P，再判断出∠DCP=∠ABD，即可得出结论；

（3）先求出BC，再判断出BD=CD，利用勾股定理求出BC=BD=，最后用△ABD∽△DCP得出比例式求解即可得出结论．

（1）如图，连接OD，

∵BC是⊙O的直径，

∴∠BAC=90°，

∵AD平分∠BAC，

∴∠BAC=2∠BAD，

∵∠BOD=2∠BAD，

∴∠BOD=∠BAC=90°，

∵DP∥BC，

∴∠ODP=∠BOD=90°，

∴PD⊥OD，

∵OD是⊙O半径，

∴PD是⊙O的切线；

（2）∵PD∥BC，

∴∠ACB=∠P，

∵∠ACB=∠ADB，

∴∠ADB=∠P，

∵∠ABD+∠ACD=180°，∠ACD+∠DCP=180°，

∴∠DCP=∠ABD，

∴△ABD∽△DCP；

（3）∵BC是⊙O的直径，

∴∠BDC=∠BAC=90°，

在Rt△ABC中，BC==13cm，

∵AD平分∠BAC，

∴∠BAD=∠CAD，

∴∠BOD=∠COD，

∴BD=CD，

在Rt△BCD中，BD2+CD2=BC2，

∴BD=CD=BC=，

∵△ABD∽△DCP，

∴，

∴，

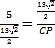∴CP=16.9cm．