题目内容
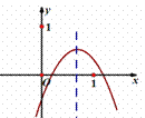
【题目】如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧，其图象与x轴交于点A（﹣1，0）与点C（x2，0），且与y轴交于点B（0，﹣2），小强得到以下结论：①0＜a＜2；②﹣1＜b＜0；③c=﹣1；④当|a|=|b|时x2＞
﹣1；以上结论中正确结论的序号为 ．
【答案】①④．
【解析】
试题由A（﹣1，0），B（0，﹣2），得b=a﹣2，∵开口向上，∴a＞0；
∵对称轴在y轴右侧，∴﹣
＞0，∴﹣
＞0，∴a﹣2＜0，∴a＜2；
∴0＜a＜2；∴①正确；
∵抛物线与y轴交于点B（0，﹣2），∴c=﹣2，故③错误；
∵抛物线图象与x轴交于点A（﹣1，0），
∴a﹣b﹣2=0，无法得到0＜a＜2；②﹣1＜b＜0，故①②错误；
∵|a|=|b|，二次函数y=ax2+bx+c的对称轴在y轴的右侧，
∴二次函数y=ax2+bx+c的对称轴为y=
，∴x2=2＞
﹣1，故④正确．
故答案为：①④．
练习册系列答案
相关题目
【题目】“文明礼仪”在人们长期生活和交往中逐渐形成，并以风俗、习惯等方式固定下来的．我们作为具有五千年文明史的“礼仪之邦”，更应该用文明的行为举止， 合理的礼仪来待人接物．为促进学生弘扬民族文化、展示民族精神，某学校开展“文明礼仪”演讲比赛，八年级（1）班，八年级（2）班各派出 5 名选手参加比赛，成绩如图所示．
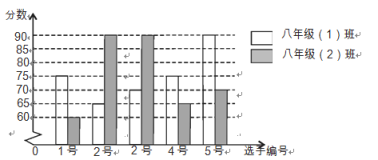
（1）根据图，完成表格：
平均数（分） | 中位数（分） | 极差（分） | 方差 | |
八年级（1）班 | 75 |
| 25 |
|
八年级（2）班 | 75 | 70 |
| 160 |
（2）结合两班选手成绩的平均分和方差，分析两个班级参加比赛选手的成绩；
（3）如果在每班参加比赛的选手中分别选出3人参加决赛，从平均分看，你认为哪个班的实力更强一些？ 说明理由．
