题目内容
【题目】请从以下(A)、(B)两题中任选一个解答.
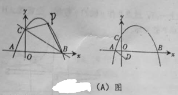
(A)已知:抛物线![]() 交
交![]() 轴于点
轴于点![]() 和点
和点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)抛物线的解析式为_____________;
(2)点![]() 为第一象限抛物线上一点,是否存在使
为第一象限抛物线上一点,是否存在使![]() 面积最大的点
面积最大的点![]() ?若不存在,请说明理由,若存在,求出点
?若不存在,请说明理由,若存在,求出点![]() 的坐标;
的坐标;
(3)点![]() 的坐标为
的坐标为![]() ,连接
,连接![]() 将线段
将线段![]() 绕平面内某一点旋转
绕平面内某一点旋转![]() 得线段
得线段![]() (点
(点![]() 分别与点
分别与点![]() 对应),使点
对应),使点![]() 都在抛物线上,请直接写点
都在抛物线上,请直接写点![]() 的坐标.
的坐标.
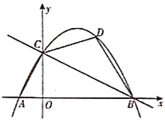
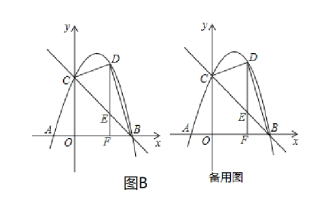
(B)如图,已知抛物线![]() 与
与![]() 轴从左至右交于
轴从左至右交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)抛物线的解析式为___________:
(2)![]() 是第一象限内抛物线上的一个动点(与点
是第一象限内抛物线上的一个动点(与点![]() 不重合),过点
不重合),过点![]() 作
作![]() 轴于点
轴于点![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() ,直线
,直线![]() 能否把
能否把![]() 分成面积之比为
分成面积之比为![]() 的两部分?若能,请求出点
的两部分?若能,请求出点![]() 的坐标;若不能,请说明理由;
的坐标;若不能,请说明理由;
(3)若![]() 为抛物线对称轴上一动点,
为抛物线对称轴上一动点,![]() 为直角三角形,请直接写出点
为直角三角形,请直接写出点![]() 的坐标.
的坐标.
我选做的是______.
【答案】选B(1)y=-x2+4x+5;(2)能. D的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );(3)(2,7),(2,-3),(2,6),(2,-1).
);(3)(2,7),(2,-3),(2,6),(2,-1).
【解析】
选B:(1)把C点坐标代入y=a(x+1)(x-5)中求出a的值即可得到抛物线解析式;
(2)先解方程-(x+1)(x-5)=0得A(-1,0),B(5,0),再利用待定系数法确定直线BC的解析式为y=-x+5,设D(x,-x2+4x+5),则E(x,-x+5),F(x,0),(0<x<5),则DE=-x2+5x,EF=-x+5,利用三角形的面积公式进行讨论:当DE:EF=2:3时,S△BDE:S△BEF=2:3;当DE:EF=3:2时,S△BDE:S△BEF=3:2,从而可得到关于x的方程,然后解方程求出x就看得到对应的D点坐标;
(3)先确定抛物线的对称轴,如图,设M(2,t),利用两点间的距离公式得到BC2=50,MC2=t2-10t+29,MB2=t2+9,利用勾股定理的逆定理分类讨论:当BC2+MC2=MB2时,△BCM为直角三角形,则50+t2-10t+29=t2+9;当BC2+MB2=MC2时,△BCM为直角三角形,则50+t2+9=t2-10t+29;当MC2+MM2=BC2时,△BCM为直角三角形,则t2-10t+29+t2+9=50,然后分别解关于t的方程,从而可得到满足条件的M点坐标.
选B:
(1)把C(0,5)代入y=a(x+1)(x-5)得-5a=5,解得a=-1,
所以抛物线解析式为y=-(x+1)(x-5),即y=-x2+4x+5;
(2)能.
当y=0时,-(x+1)(x-5)=0,解得x1=-1,x2=5,则A(-1,0),B(5,0),
设直线BC的解析式为y=kx+b,
把C(0,5),B(5,0)代入得![]() ,解得
,解得![]() ,
,
所以直线BC的解析式为y=-x+5,
设D(x,-x2+4x+5),则E(x,-x+5),F(x,0),(0<x<5),
∴DE=-x2+4x+5-(-x+5)=-x2+5x,EF=-x+5,
当DE:EF=2:3时,S△BDE:S△BEF=2:3,即(-x2+5x):(-x+5)=2:3,
整理得3x2-17x+10=0,解得x1=![]() ,x2=5(舍去),此时D点坐标为(
,x2=5(舍去),此时D点坐标为(![]() ,
,![]() );
);
当DE:EF=3:2时,S△BDE:S△BEF=3:2,即(-x2+5x):(-x+5)=3:2,
整理得2x2-13x+15=0,解得x1=![]() ,x2=5(舍去),此时D点坐标为(
,x2=5(舍去),此时D点坐标为(![]() ,
,![]() );
);
综上所述,当点D的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )时,直线BC能否把△BDF分成面积之比为2:3的两部分;
)时,直线BC能否把△BDF分成面积之比为2:3的两部分;
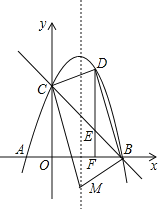
(3)抛物线的对称轴为直线x=2,如图,
设M(2,t),
∵B(5,0),C(0,5),
∴BC2=52+52=50,MC2=22+(t-5)2=t2-10t+29,MB2=(2-5)2+t2=t2+9,
当BC2+MC2=MB2时,△BCM为直角三角形,∠BCM=90°,即50+t2-10t+29=t2+9,解得t=7,此时M点的坐标为(2,7);
当BC2+MB2=MC2时,△BCM为直角三角形,∠CBM=90°,即50+t2+9=t2-10t+29,解得t=-3,此时M点的坐标为(2,-3);
当MC2+MM2=BC2时,△BCM为直角三角形,∠CMB=90°,即t2-10t+29+t2+9=50,解得t1=6,t2=-1,此时M点的坐标为(2,6)或(2,-1),
综上所述,满足条件的M点的坐标为(2,7),(2,-3),(2,6),(2,-1).