Question

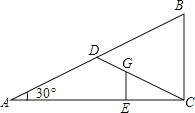
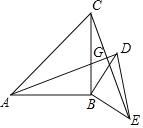
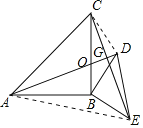
【题目】如图，△ABC和△BED都是等腰直角三角形，∠ABC=∠DBE=90°，AD，CE相交于点G

（1）求证：△ABD≌△CBE；

（2）求证：AD⊥CE；

（3）连接AE，CD，若AE=CD=5，求△ABC和△BED的面积之和．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）．

【解析】

（1）根据SAS证明△ABD≌△CBE即可；

（2）设AD交BC于点O．由△ABD≌△CBE，推出∠BAD=∠BCE，由∠BAO+∠AOB=90°，∠AOB=∠COG，推出∠COG+∠OCG=90°，可得∠OGC=90°；

（3）连接AE，CD．利用勾股定理求出2AB2+2BD2=30即可解决问题；

（1）证明：∵∠ABC=∠DBE=90°，

∴∠ABD=∠CBE，

在△ABD和△CBE中，

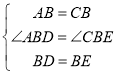
∴△ABD≌△CBE（SAS）．

（2）证明：设AD交BC于点O．

∵△ABD≌△CBE，

∴∠BAD=∠BCE，

∵∠BAO+∠AOB=90°，∠AOB=∠COG，

∴∠COG+∠OCG=90°，

∴∠OGC=90°，

∴AD⊥CE．

（3）连接AE，CD．

∵AD⊥EC，

∴∠CGD=∠AGE=90°

∴CG2+DG2=CD2，AG2+GE2=AE2，

∵CD=，AE=5，

∴CG2+DG2+AG2+GE2=30，

∴AC2+DE2=30，

∴2AB2+2BD2=30，

∴AB2+BD2=15，

∵S△ABC+S△BDE=AB2+BD2=（AB2+BD2）=．