题目内容
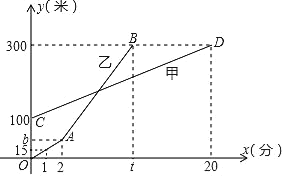
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?
【答案】(1)10;30;(2)y=![]() ;(3)登山3分钟、10分钟或13分钟
;(3)登山3分钟、10分钟或13分钟
【解析】
(1)根据速度=高度÷时间即可算出甲登山上升的速度; 根据高度=速度×时间即可算出乙在A地时距地面的高度b的值;
(2)分0≤x≤2和x≥2两种情况,根据高度=初始高度+速度×时间即可得出y关于x的函数关系;
(3)当乙未到终点时, 找出甲登山全程中y关于x的函数关系式,令二者做差等于50即可得出关于x的一元一次方程, 解之即可求出x值;当乙到达终点时,用终点的高度-甲登山全程中y关于x的函数关系式=50,即可得出关于x的一元一次方程, 解之可求出x值.综上即可得出结论.
(1)甲登山上升的速度是:(300﹣100)÷20=10(米/分钟),
b=15÷1×2=30.
故答案为:10;30;
(2)当0≤x<2时,y=15x;
当x≥2时,y=30+10×3(x﹣2)=30x﹣30.
当y=30x﹣30=300时,x=11.
∴乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=![]() ;
;
(3)甲登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=10x+100(0≤x≤20).
当10x+100﹣(30x﹣30)=70时,解得:x=3;
当30x﹣30﹣(10x+100)=70时,解得:x=10;
当300﹣(10x+100)=70时,解得:x=13.
答:登山3分钟、10分钟或13分钟时,甲、乙两人距地面的高度差为70米.

 学而优衔接教材南京大学出版社系列答案
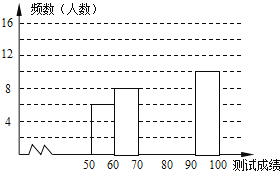
学而优衔接教材南京大学出版社系列答案【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数 |
第1组 |
| 6 |
第2组 |
| 8 |
第3组 |
| 14 |
第4组 |
| a |
第5组 |
| 10 |
请结合图表完成下列各题:
![]() 求表中a的值;
求表中a的值; ![]() 频数分布直方图补充完整;
频数分布直方图补充完整;
![]() 若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
![]() 第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.