Question

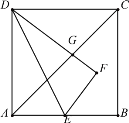
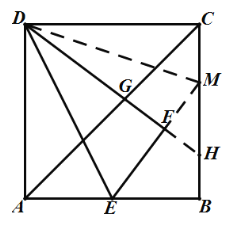
【题目】如图，正方形ABCD的边长为4，E为AB的中点，将△ADE沿直线DE折叠后，点A落在点F处，DF交对角线AC于G，则FG的长是________．

Answer 1

【答案】

【解析】

延长DF，EF分别交BC于H，M，连接DM，根据折叠的性质得到DA=DF，∠DAE=∠DFE=90°，根据全等三角形的性质得到CM=FM，设CM=FM=x，则BM=4x，EM=2+x，根据勾股定理列出方程求出x，从而得到CM=FM=，根据相似三角形的判定与性质即可得到结论．

解：延长DF，EF分别交BC于H，M，连接DM，

∵四边形ABCD是正方形，

∴DA=DC，∠DAE=∠DCB=90°，

∵将沿直线DE折叠后，点A落在点F处，

∴，

∴，

∵，

∴，

∴，,

∵正方形ABCD的边长为4，E为AB的中点，

∴，

设，则BM=4x，EM=2+x，

在中，由勾股定理得：，

即，解得：，

∴，，，

∵，，

∴，

∴，即，

解得：，，

∴，，

∵，

∴，

∴，即，

∴，

∴，

故答案为：．