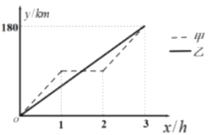
题目内容
【题目】如图,先将正方形纸片儿对折,折痕为MN,再把点B折叠在折痕MN上,折痕为AE,点E在CB上,点B在MN上的对应点为H,沿AH和DH剪下得到三角形ADH,则下列选项错误的是( )
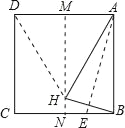
A. DH=AD B. AH=DH C. NE=BE D. DM=![]() DH
DH
【答案】C
【解析】分析:利用折叠的性质可得,AB=AH,AH=DH, BE=HE,DM=![]() AD,结合正方形的性质可得A、B、C正确,根据垂线段最短可得C错误.
AD,结合正方形的性质可得A、B、C正确,根据垂线段最短可得C错误.
详解:如图,连结EH,
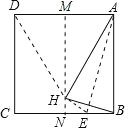
由折叠得性质可知:AB=AH,AH=DH, BE=HE,DM=![]() AD,
AD,
∴AB=AH =DH,
又∵AB=AD,
∴AD=AH =DH,
故A、B正确;
∵BE=HE,HE>NE,
∴BE=NE,
故C不正确;
∵DM=![]() AD,AD= DH,
AD,AD= DH,
∴DM=![]() DH,
DH,
故D正确;
故选:C.

练习册系列答案
相关题目