题目内容
【题目】在平面直角坐标系中,点![]() ,在
,在![]() 轴上任取一点
轴上任取一点![]() ,连接
,连接![]() ,作
,作![]() 的垂直平分线
的垂直平分线![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,
,![]() 与
与![]() 交于点
交于点![]() .设
.设![]() 点的坐标为
点的坐标为![]() .
.
(Ⅰ)当![]() 的坐标取
的坐标取![]() 时,点
时,点![]() 的坐标为________;
的坐标为________;
(Ⅱ)求![]() ,
,![]() 满足的关系式;
满足的关系式;
(Ⅲ)是否存在点![]() ,使得
,使得![]() 恰为等边三角形?若存在,求点
恰为等边三角形?若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)存在,
;(Ⅲ)存在,![]() ,
, ![]() .
.
【解析】
(Ⅰ)作AN⊥PM于N,根据线段垂直平分线的性质得到PA=PM,根据勾股定理计算;
(Ⅱ)分点M在x轴的正半轴上、点M在x轴的负半轴上两种情况,根据勾股定理列式计算;
(Ⅲ)根据勾股定理求出MA,根据(Ⅱ)中结论列出方程,解方程即可.
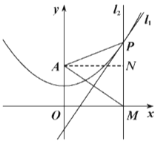
(Ⅰ)作AN⊥PM于N,
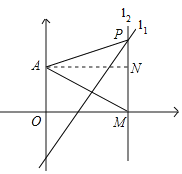
则四边形AOMN是矩形,
∴AN=OM=3,MN=OA=2,
∵l1是AM的垂直平分线,
∴PA=PM,
在Rt△APN中,AN2+PN2=AP2,即32+(y-2)2=y2,
解得,y=![]() ,
,
∴点P的坐标为(3,![]() ),
),
故答案为:(3,![]() );
);
(Ⅱ)如图,过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,
,
可得![]() 为矩形,可得
为矩形,可得![]() ,
,
∵![]() 轴,
轴,![]() 点的坐标为
点的坐标为![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,![]() ,
,
∵点![]() 在
在![]() 的垂直平分线
的垂直平分线![]() 上,
上,
∴![]() ,
,
在![]() 中,
中,![]() ,且
,且![]() ,
,
∴![]() ,
,
∴![]() .
.
(Ⅲ)由(Ⅱ)知,![]() ,要使△MPA为等边三角形,只需MA=MP即可,
,要使△MPA为等边三角形,只需MA=MP即可,
∵点A的坐标为(0,2),点M的坐标为(0,x),
∴AM=![]() ,
,
则![]() ,
,
解得,x=±2![]() ,
,
∴![]() 或
或![]() .
.

练习册系列答案
相关题目