Question

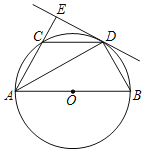
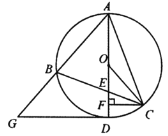
【题目】如图，已知内接于⊙，直径交于点，连接，过点作，垂足为．过点作⊙的切线，交的延长线于点．

(1)若，求的度数；

(2)若，求证：；

(3)在(2)的条件下，连接，设的面积为，的面积为，若，求的值

Answer 1

【答案】（1）50°；（2）详见解析；（3）

【解析】

（1）连接BD，如图，利用切线性质和圆周角定理得到∠ADG=∠ABD=90°，再利用等角的余角相等得到∠ADB=∠G=50°，然后根据圆周角定理得到∠ACB的度数；

（2）连接CD，如图，利用等腰三角形的性质得到∠ABE=∠AEB，∠ODC=∠OCD，再利用圆周角定理得到∠ABC=∠ADC，然后根据三角形内角和可判断∠BAD=∠DOC；

（3）先证明△ABD∽△OFC得到,设则 则利用三角形面积公式得到则可设OF=4k，则OA=5k，利用勾股定理计算出CF，然后根据正切的定义求解．

（1）解：连接BD，如图，

∵DG为切线，

∴AD⊥DG， ∴∠ADG=90°，

∵AD为直径， ∴∠ABD=90°，

∠GDB+∠G=90°，∠ADB+∠GDB=90°，

∴∠ADB=∠G=50°，

∴∠ACB=∠ADB=50°；

（2）证明：连接CD，如图，

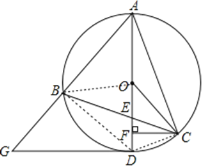
∵AB=AE， ∴∠ABE=∠AEB，

∵OD=OC， ∴∠ODC=∠OCD，

而∠ABC=∠ADC， ∴∠ABE=∠AEB=∠ODC=∠OCD，

∴∠BAD=∠FOC；

（3）解：∵∠BAD=∠FOC，∠ABD=∠OFC，

∴△ABD∽△OFC，

∴，

∵

设 则

∴

∴

∵

∴设OF=4k，则OA=5k，

在Rt△OCF中，OC=5k， CF=

∴tan∠CAF=