ĖâÄŋÄÚČÝ
ĄūĖâÄŋĄŋÎŌÃĮÖŠĩĀĢŽÆ―ÃæÄÚŧĨÏāīđÖąĮŌÓÐđŦđēÔĩãĩÄÁ―ĖõĘýÖáđđģÉÆ―ÃæÖą―ĮŨøąęÏĩĢŽČįđûÁ―ĖõĘýÖáēŧīđÖąĢŽķøĘĮÏā―ŧģÉČÎŌâĩÄ―ĮĶØĢĻ0ĄãĢžĶØĢž180ĄãĮŌĶØĄŲ90ĄãĢĐĢŽÄĮÃīÕâÁ―ĖõĘýÖáđđģÉĩÄĘĮÆ―ÃæÐąŨøąęÏĩĢŽÁ―ĖõĘýÖáģÆÎŠÐąŨøąęÏĩĩÄŨøąęÖáĢŽđŦđēÔĩãģÆÎŠÐąŨøąęÏĩĩÄÔĩãĢŽČįÍž1ĢŽūđýÆ―ÃæÄÚŌŧĩãPŨũŨøąęÖáĩÄÆ―ÐÐÏßPMšÍPNĢŽ·Öąð―ŧxÖášÍyÖáÓÚĩãMĢŽNĢŪĩãMĄĒNÔÚxÖášÍyÖáÉÏËųķÔÓĶĩÄĘý·Öąð―ÐŨöPĩãĩÄxŨøąęšÍyŨøąęĢŽÓÐÐōĘĩĘýķÔĢĻxĢŽyĢĐģÆΊĩãPĩÄÐąŨøąęĢŽžĮΊPĢĻxĢŽyĢĐ

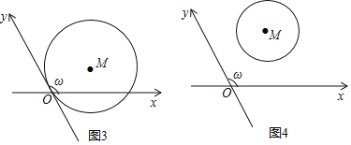
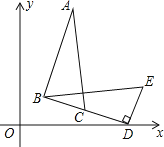
ĢĻ1ĢĐČįÍž2ĢŽĶØĢ―45ĄãĢŽūØÐÎOABCÖÐĩÄŌŧąßOAÔÚxÖáÉÏĢŽBCÓëyÖá―ŧÓÚĩãDĢŽ
OAĢ―2ĢŽOCĢ―1ĢŪ
ĒŲĩãAĄĒBĄĒCÔÚīËÐąŨøąęÏĩÄÚĩÄŨøąę·ÖąðΊAĄĄĄĄĢŽBĄĄĄĄĢŽCĄĄĄĄĢŪ
ĒÚÉčĩãPĢĻxĢŽyĢĐÔÚūđýOĄĒBÁ―ĩãĩÄÖąÏßÉÏĢŽÔōyÓëxÖŪžäÂúŨãĩÄđØÏĩΊĄĄĄĄĢŪ
ĒÛÉčĩãQĢĻxĢŽyĢĐÔÚūđýAĄĒDÁ―ĩãĩÄÖąÏßÉÏĢŽÔōyÓëxÖŪžäÂúŨãĩÄđØÏĩΊĄĄĄĄĢŪ
ĢĻ2ĢĐČôĶØĢ―120ĄãĢŽOΊŨøąęÔĩãĢŪ
ĒŲČįÍž3ĢŽÔēMÓëyÖáÏāĮÐÔĩãOĢŽąŧxÖá―ØĩÃĩÄÏŌģĪOAĢ―2![]() ĢŽĮóÔēMĩÄ°ëūķž°ÔēÐÄMĩÄÐąŨøąęĢŪ
ĢŽĮóÔēMĩÄ°ëūķž°ÔēÐÄMĩÄÐąŨøąęĢŪ
ĒÚČįÍž4ĢŽÔēMĩÄÔēÐÄÐąŨøąęΊMĢĻ2![]() ĢŽ2
ĢŽ2![]() ĢĐĢŽČôÔēÉÏĮĄÓÐÁ―ļöĩãĩ―yÖáĩÄūāĀëΊ1ĢŽÔōÔēMĩÄ°ëūķrĩÄČĄÖĩ·ķΧĘĮĄĄĄĄĢŪ
ĢĐĢŽČôÔēÉÏĮĄÓÐÁ―ļöĩãĩ―yÖáĩÄūāĀëΊ1ĢŽÔōÔēMĩÄ°ëūķrĩÄČĄÖĩ·ķΧĘĮĄĄĄĄĢŪ
Ąūīð°ļĄŋĢĻ1ĢĐĒŲĢĻ2ĢŽ0ĢĐĢŽĢĻ1ĢŽ![]() ĢĐĢŽĢĻĐ1ĢŽ
ĢĐĢŽĢĻĐ1ĢŽ![]() ĢĐĢŧĒÚyĢ―
ĢĐĢŧĒÚyĢ―![]() xĢŧĒÛyĢ―Đ
xĢŧĒÛyĢ―Đ![]() x+
x+![]() Ģŧ
Ģŧ
ĢĻ2ĢĐĒŲ°ëūķΊ2ĢŽMĢĻ![]() ĢĐĢŧĒÚ2ĢžrĢž4
ĢĐĢŧĒÚ2ĢžrĢž4
Ąū―âÎöĄŋ
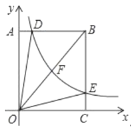
ĢĻ1ĢĐĒŲČįÍž21ÖÐĢŽŨũBEĄÎOD―ŧOAÓÚEĢŽCFĄÎOD―ŧxÖáÓÚFĢŪĮóģöOEĄĒOFĄĒCFĄĒODĄĒBEžīŋÉ―âūöÎĘĖâĢŧ
ĒÚČįÍž22ÖÐĢŽŨũBEĄÎOD―ŧOAÓÚEĢŽŨũPMĄÎOD―ŧOAÓÚMĢŪĀûÓÃÆ―ÐÐÏß·ÖÏßķÎģÉąČĀýķĻĀížīŋÉ―âūöÎĘĖâĢŧ
ĒÛČįÍž33ÖÐĢŽŨũQMĄÎOA―ŧODÓÚMĢŪĀûÓÃÆ―ÐÐÏß·ÖÏßķÎģÉąČĀýķĻĀížīŋÉ―âūöÎĘĖâĢŧ
ĢĻ2ĢĐĒŲČįÍž3ÖÐĢŽŨũMFĄÍOAÓÚFĢŽŨũMNĄÎyÖá―ŧOAÓÚNĢŪ―âÖą―ĮČý―ĮÐΞīŋÉ―âūöÎĘĖâĢŧ
ĒÚČįÍž4ÖÐĢŽÁŽ―ÓOMĢŽŨũMKĄÎxÖá―ŧyÖáÓÚKĢŽŨũMNĄÍOKÓÚN―ŧĄŅMÓÚEĄĒFĢŪĮóģöFNĢ―NEĢ―1ĘąĢŽĄŅMĩÄ°ëūķžīŋÉ―âūöÎĘĖâĢŧ
―âĢšĢĻ1ĢĐĒŲČįÍž2Đ1ÖÐĢŽŨũBEĄÎOD―ŧOAÓÚEĢŽCFĄÎOD―ŧxÖáÓÚFĢŪ
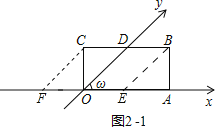
ÓÉĖâŌâOCĢ―CDĢ―1ĢŽOAĢ―BCĢ―2ĢŽ
ĄāBDĢ―OEĢ―1ĢŽODĢ―CFĢ―BEĢ―![]() ĢŽ
ĢŽ
ĄāA(2,0)ĢŽB(1,![]() )ĢŽC(Đ1,
)ĢŽC(Đ1,![]() )ĢŽ
)ĢŽ
đĘīð°ļΊĢšA(2,0)ĢŽB(1,![]() )ĢŽC(Đ1,
)ĢŽC(Đ1,![]() )ĢŪ
)ĢŪ
ĒÚČįÍž2Đ2ÖÐĢŽŨũBEĄÎOD―ŧOAÓÚEĢŽŨũPMĄÎOD―ŧOAÓÚMĢŪ
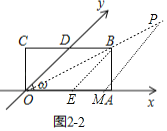
ĄßODĄÎBEĢŽODĄÎPMĢŽ
ĄāBEĄÎPMĢŽ
Ąā![]() ĢŽ
ĢŽ
Ąā![]() ĢŽ
ĢŽ
ĄāyĢ―![]() xĢŪ
xĢŪ
đĘīð°ļΊĢšyĢ―![]() xĢŪ
xĢŪ
ĒÛČįÍž2Đ3ÖÐĢŽŨũQMĄÎOA―ŧODÓÚMĢŪ
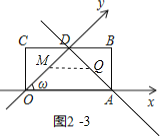
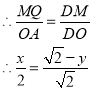
Ąā![]()
đĘīð°ļΊĢšyĢ―Đ![]() x+
x+![]() ĢŪ
ĢŪ
ĢĻ2ĢĐĒŲČįÍž3ÖÐĢŽŨũMFĄÍOAÓÚFĢŽŨũMNĄÎyÖá―ŧOAÓÚNĢŪ
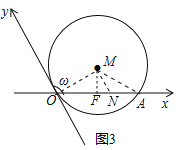
ĄßĶØĢ―120ĄãĢŽOMĄÍyÖáĢŽ
ĄāĄÏMOAĢ―30ĄãĢŽ
ĄßMFĄÍOAĢŽOAĢ―![]() ĢŽ
ĢŽ
ĄāOFĢ―FAĢ―![]() ĢŽ
ĢŽ
ĄāFMĢ―1ĢŽOMĢ―2FMĢ―2ĢŽ
ĄāÔēMĩÄ°ëūķΊ2
ĄßMNĄÎyÖáĢŽ
ĄāMNĄÍOMĢŽ
ĄāMNĢ―![]() ĢŽONĢ―2MNĢ―
ĢŽONĢ―2MNĢ―![]() ĢŽ
ĢŽ
ĄāM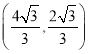 ĢŪ
ĢŪ
ĒÚČįÍž4ÖÐĢŽÁŽ―ÓOMĢŽŨũMKĄÎxÖá―ŧyÖáÓÚKĢŽŨũMNĄÍOKÓÚN―ŧĄŅMÓÚEĄĒFĢŪ
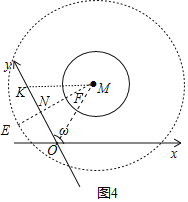
ĄßMKĄÎxÖáĢŽĶØĢ―120ĄãĢŽ
ĄāĄÏMKOĢ―60ĄãĢŽ
ĄßMKĢ―OKĢ―2![]() ĢŽ
ĢŽ
ĄāĄũMKOĘĮĩČąßČý―ĮÐÎĢŽ
ĄāMNĢ―3ĢŽ
ĩąFNĢ―1ĘąĢŽMFĢ―3Đ1=2ĢŽ
ĩąENĢ―1ĘąĢŽMEĢ―3+1=4ĢŽ
đÛēėÍžÏóŋÉÖŠĩąĄŅMĩÄ°ëūķrĩÄČĄÖĩ·ķΧΊ2ĢžrĢž4ĢŪ
đĘīð°ļΊĢš2ĢžrĢž4ĢŪ