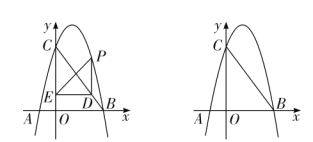
题目内容
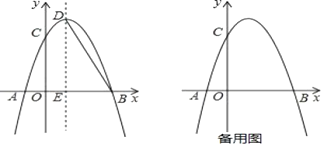
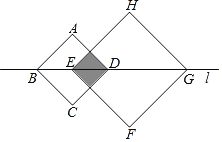
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
(1)求抛物线的解析式;
(2)点![]() 是抛物线上一点,设
是抛物线上一点,设![]() 点的横坐标为
点的横坐标为![]() .
.
①当点![]() 在第一象限时,过点
在第一象限时,过点![]() 作
作![]() 轴,交
轴,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() ,当
,当![]() 和
和![]() 相似时,求点
相似时,求点![]() 的坐标;
的坐标;
②请直接写出使![]() 的点
的点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)①点
;(2)①点![]() 的坐标为
的坐标为![]() 或
或![]() ;②点
;②点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)将![]() 、
、![]() 两点坐标代入抛物线
两点坐标代入抛物线![]() ,列出关于a和b的方程组求解即可;(2)①设
,列出关于a和b的方程组求解即可;(2)①设![]() ,由点
,由点![]() 和点
和点![]() 可得
可得![]() 的表达式,分两种情况:当
的表达式,分两种情况:当![]() 时和当
时和当![]() 时根据相似三角形的性质求解即可;
时根据相似三角形的性质求解即可;
②如图,过点B作∠ABC的角平分线分别交y轴、抛物线于点M、P,在x轴的下方作![]() ,设点M的坐标为(0,k),求出点M的坐标,得出直线BM的解析式,联立方程,求出点P的坐标,同理可得点
,设点M的坐标为(0,k),求出点M的坐标,得出直线BM的解析式,联立方程,求出点P的坐标,同理可得点![]() .
.
(1)将![]() 、
、![]() 两点坐标代入抛物线
两点坐标代入抛物线![]() 解析式,
解析式,
可得![]() ,解得
,解得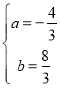 ,
,
∴抛物线的解析式为![]() ;
;
(2)①设![]() ,
,
由点![]() 和点
和点![]() 可得
可得![]() 的表达式:
的表达式:![]() ,
,
![]()
则![]() ,
,
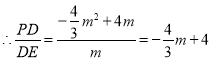 ,
,
![]() 轴,
轴,![]() 轴,
轴,
![]() ,
,
(Ⅰ)当![]() 时,
时,![]() ,
,
则![]() ,
,
![]()
(Ⅱ)当![]() 时,
时,![]() ,
,
则![]() ,
,
![]() ,
,
∴当![]() 与
与![]() 相似时,点
相似时,点![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
②如图,过点B作∠ABC的角平分线分别交y轴、抛物线于点M、P,在x轴的下方作∠ABP= ![]() ∠ABC,设点M的坐标为(0,k),
∠ABC,设点M的坐标为(0,k),
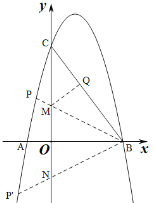
∵OB=3,OC=4,
∴BC=5,
∵BM平分∠ABC,
∴MO=MQ,
∴![]() ,
,
即![]() ,
,
解得![]() ,点M的坐标为(0,
,点M的坐标为(0,![]() ),
),
∴直线BM的解析式为![]() ,
,
联立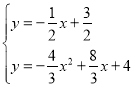 ,
,
解得![]() 或
或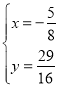 ,
,
∴点P的坐标为![]() ,
,
由作图可知,M与点N关于x轴对称,
∴点N的坐标为(0,![]() ),
),
同理可得点![]() 的坐标为
的坐标为![]() ,
,
综上点P的坐标为![]() 或
或![]() .
.

【题目】某校随机抽查了部分九年级女生进行1分钟仰卧起坐测试,并将测试的结果绘制成了如图的不完整的统计表和频数分布直方图(注:在频数分布直方图中,每组含左端点,但不含右端点):
仰卧起坐次数的范围(次) | 15~20 | 20~25 | 25~30 | 30~35 |
频数 | 3 | 10 | 12 |
|
频率 |
|
|
|
|

(1)30~35的频数是 、25~30的频率是 .并把统计图补充完整;
(2)被抽查的所有女同学仰卧起坐次数的中位数是多少?