题目内容
【题目】【探究证明】
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
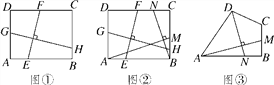
如图①,在矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证: ![]() ;
;
【结论应用】
(2)如图②,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若![]() ,则
,则![]() 的值为 ;
的值为 ;
【联系拓展】
(3)如图③,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析: (1)过点A作AP∥EF,交CD于P,过点B作BQ∥GH,交AD于Q,如图1,易证AP=EF,GH=BQ,△PDA∽△QAB,然后运用相似三角形的性质就可解决问题,
(2)只需运用(1)中的结论,就可得到![]() ,就可解决问题,
,就可解决问题,
(3)过点D作平行于AB的直线,交过点A平行于BC的直线于R,交BC的延长线于S,如图3,易证四边形ABSR是矩形,由(1)中的结论可得=.设SC=x,DS=y,则AR=BS=5+x,RD=10﹣y,在Rt△CSD中根据勾股定理可得![]() ①,在Rt△ARD中根据勾股定理可得
①,在Rt△ARD中根据勾股定理可得![]() +
+![]() =100②,解①②就可求出x,即可得到AR,问题得以解决.
=100②,解①②就可求出x,即可得到AR,问题得以解决.
试题解析: (1)过点A作AP∥EF,交CD于P,过点B作BQ∥GH,交AD于Q,如图1,
∵四边形ABCD是矩形,
∴AB∥DC,AD∥BC,
∴四边形AEFP,四边形BHGQ都是平行四边形,
∴AP=EF,GH=BQ,
又∵GH⊥EF,
∴AP⊥BQ,
∴∠QAT+∠AQT=90°,
∵四边形ABCD是矩形,
∴∠DAB=∠D=90°,
∴∠DAP+∠DPA=90°,
∴∠AQT=∠DPA,
∴△PDA∽△QAB,
∴![]() ,
,
∴![]() ,
,
(2)如图2,
∵EF⊥GH,AM⊥BN,
∴由(1)中的结论可得![]() ,
,![]() ,
,
∴![]()
故答案为: ![]() ,
,
(2)过点D作平行于AB的直线,交过点A平行于BC的直线于R,交BC的延长线于S,如图3,则四边形ABSR是平行四边形,
∵∠ABC=90°,
∴ABSR是矩形,
∴∠R=∠S=90°,RS=AB=10,AR=BS,
∵AM⊥DN,
∴由(1)中的结论可得![]() ,
,
设SC=x,DS=y,则AR=BS=5+x,RD=10﹣y,
∴在Rt△CSD中,x2+y2=25①,
在Rt△ARD中,(5+x)2+(10﹣y)2=100②,
由②﹣①得x=2y﹣5③,
解方程组![]() 得
得
![]() (舍去),或
(舍去),或![]() ,
,
∴AR=5+x=8,
∴![]() .
.

【题目】某文具店准备购进A、B两种型号的书包共50个进行销售,两种书包的进价、售价如下表所示:
书包型号 | 进价(元/个) | 售价(元/个) |
A型 | 200 | 300 |
B型 | 100 | 150 |
购进这50个书包的总费用不超过7300元,且购进B型书包的个数不大于A型书包个数的![]() .
.
(1)该文具店有哪几种进货方案?
(2)若该文具店购进的50个书包全部售完,则该文具店采用哪种进货方案,才能获得最大利润?最大利润是多少?(利润=售价﹣进价)



