题目内容
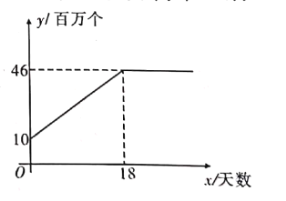
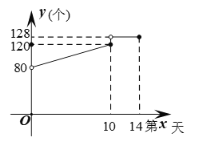
【题目】某厂家接到一批特殊产品的生产订单,客户要求在两周内完成生产,并商定这批产品的出厂价为每个16元.受市场影响,制造这批产品的某种原材料成本价持续上涨,设第x天(1≤x≤14,且x为整数)每个产品的成本为m元,m与x之间的函数关系为m=![]() x+8.订单完成后,经统计发现工人王师傅第x天生产的产品个数y与x满足如图所示的函数关系:
x+8.订单完成后,经统计发现工人王师傅第x天生产的产品个数y与x满足如图所示的函数关系:
(1)写出y与x之间的函数关系式及自变量x的取值范围;
(2)设王师傅第x天创造的产品利润为W元,问王师傅第几天创造的利润最大?最大利润是多少元?
【答案】(1)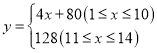 且x为正整数;(2)王师傅第
且x为正整数;(2)王师傅第![]() 天创造的利润最大,最大利润是
天创造的利润最大,最大利润是![]() 元
元
【解析】
(1)首先观察题中的函数图像可知其为一个分段函数,由此分别表示出![]() 时与
时与![]() 时两个范围内的函数关系式,并且其中x为正整数,由此进一步即可得出答案;
时两个范围内的函数关系式,并且其中x为正整数,由此进一步即可得出答案;
(2)根据题意分当![]() 且x为正整数时或当
且x为正整数时或当![]() 且x为正整数时两种情况进一步分析比较即可.
且x为正整数时两种情况进一步分析比较即可.
(1)由题意可得,![]() ,
,
∴当![]() 且x为正整数时,y与x之间的函数关系式为:
且x为正整数时,y与x之间的函数关系式为:![]() ,
,
当![]() 且x为正整数时,y与x之间的函数关系式为:
且x为正整数时,y与x之间的函数关系式为:![]() ,
,
综上所述,y与x之间的函数关系式为: 且x为正整数;
且x为正整数;
(2)①当![]() 且x为正整数时,
且x为正整数时,
![]() ,
,
∵![]() ,
,![]() ,
,
∴当![]() 时,
时,![]() ,
,
②当![]() 时,且
时,且![]() 为正整数时,
为正整数时,
![]() ,
,
∵![]() ,
,
∴![]() 随
随![]() 的增大而减小,
的增大而减小,
∴当![]() 时,
时,![]()
∵![]() ,
,
∴王师傅第![]() 天创造的利润最大,最大利润是
天创造的利润最大,最大利润是![]() 元,
元,
答:王师傅第![]() 天创造的利润最大,最大利润是
天创造的利润最大,最大利润是![]() 元.
元.

【题目】如图,Rt△ACB中,∠ACB=90°,AC=2BC=4,点P为AB边中点,点E为AC边上不与端点重合的一动点,将△ADP沿着直线PD折叠得△PDE,若DE⊥AB,则AD的长度为_____ .
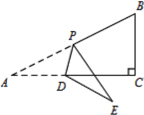
【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级成绩频数分布直方图:
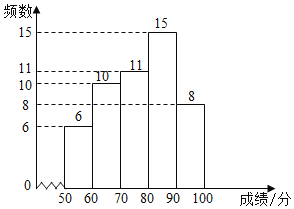
b.七年级成绩在![]() 这一组的是:70 72 74 75 76 76 77 77 77 78 79
这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级 | 平均数 | 中位数 |
七 | 76.9 | m |
八 | 79.2 | 79.5 |
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;
(4)该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.