题目内容
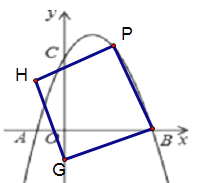
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 是抛物线的顶点,过点
是抛物线的顶点,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() .
.
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)点![]() 是抛物线上的动点,当
是抛物线上的动点,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
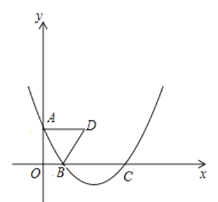
(3)若点![]() 是
是![]() 轴上方抛物线上的动点,以
轴上方抛物线上的动点,以![]() 为边作正方形
为边作正方形![]() ,随着点
,随着点![]() 的运动,正方形的大小、位置也随着改变,当顶点
的运动,正方形的大小、位置也随着改变,当顶点![]() 或
或![]() 恰好落在
恰好落在![]() 轴上时,请直接写出点
轴上时,请直接写出点![]() 的横坐标.
的横坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 点的坐标为
点的坐标为![]() 或
或![]() ;(3)点
;(3)点![]() 的横坐标为
的横坐标为![]() 或0或2或
或0或2或![]() .
.
【解析】
(1)将点B、C坐标代入可求得解析式,将二次函数转化为顶点式,得出顶点;
(2)过![]() 作
作![]() 轴于点
轴于点![]() ,设出点F的坐标,利用
,设出点F的坐标,利用![]() 可得结果;
可得结果;
(3)分2种情况讨论,一种是点G在y轴上,另一种是H在y轴上,利用矩正方形夹角为90°和邻边相等的性质可求得.
(1)把点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() 代入抛物线
代入抛物线![]() 得:
得:
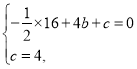 解得:
解得:![]()
∴![]() ,
,
∴![]() ;
;
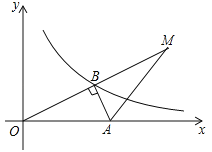
(2)如图,在线段![]() 上选取点
上选取点![]() ,使得
,使得![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() .
.
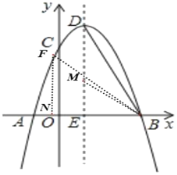
此时![]() .
.
设![]() ,
,
在![]() 中,
中,
![]() .
.
即![]() .
.
解得![]() .
.
∴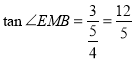 .
.
设![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
即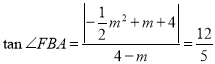 ,
,
当点![]() 在
在![]() 轴上方时,有
轴上方时,有![]() ,
,
解得![]() (舍去),
(舍去),![]() ,
,
此时![]() 点的坐标为
点的坐标为![]() ;
;
当点![]() 在
在![]() 轴下方时,有
轴下方时,有![]() ,
,
解得![]() (舍去),
(舍去),![]() ,
,
此时![]() 点的坐标为
点的坐标为![]() ;
;
综上可知![]() 点的坐标为
点的坐标为![]() 或
或![]() ;
;
(3)情况一:点G在y轴上
设点P(m,![]() )
)
∵![]()
∴点P(m,![]() )
)
∵点B(4,0)
∴根据B、P两点可得PB的解析式为:![]()
∵四边形PHGB是矩形,∴BG⊥PB
∴直线BG的解析式中,k=![]()
将点B代入BG的解析式,可求得BG的解析式为:![]()
∵点G在y轴上,令x=0,解得:y=![]()
∴G(0,![]() )
)
∵四边形PHGB是矩形,∴PB=BG,![]()
根据点B、P的坐标得:![]()
根据点B、G的坐标得:
另![]() ,即
,即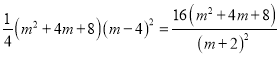
∵![]()
∴化简得:![]()
a.(m-4)(m+2)=8
解得:m=1+![]() (舍),或m=1-
(舍),或m=1-![]() (舍)
(舍)
b.(m-4)(m+2)=-8
解得:m=0,或m=2
情况二:点H在y轴上

同上:点P(m,![]() ),点B(4,0),根据B、P两点可得PB的解析式为:
),点B(4,0),根据B、P两点可得PB的解析式为:![]() ,
,![]()
∵四边形PHGB是矩形,∴PH⊥PB
∴PH解析式的k=![]()
将点P代入PH的解析式,可求得PH的解析式为:![]()
∴H(0,![]() )
)
根据点P、H的坐标得: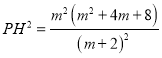
同理,![]() ,即:
,即: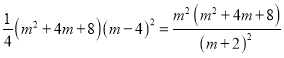
化简得: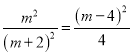
a.![]()
解得:m=2+![]() (舍),或m=2-2
(舍),或m=2-2![]()
b.![]()
解得:m=2![]() ,或m=-2
,或m=-2![]() (舍)
(舍)
综上得:点![]() 的横坐标为
的横坐标为![]() 或0或2或
或0或2或![]()

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案【题目】为迎接2022年冬奥会,鼓励更多的大学生参与到志愿服务中,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有300名学生进入综合素质展示环节,为了了解这些学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
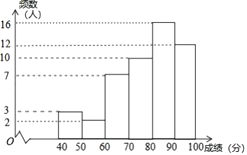
a.甲学校学生成绩的频数分布直方图如图(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
b.甲学校学生成绩在![]() 这一组是:
这一组是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
83.3 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生![]() ,乙学校学生
,乙学校学生![]() 的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“
的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“![]() ”或“
”或“![]() ”);
”);
(2)根据上述信息,推断________学校综合素质展示的水平更高,理由为:__________________________
(至少从两个不同的角度说明推断的合理性).
(3)若每所学校综合素质展示的前120名学生将被选入志愿服务团队,预估甲学校分数至少达到________分的学生才可以入选.