题目内容
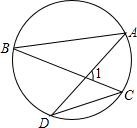
如图，⊙O是△ABC的外接圆，AD是△ABC的高，AE是⊙O的直径，求证：∠BAE=∠CAD．
证明：连接BE，
∵AE是⊙O的直径，
∴∠ABE=90°．
∴∠BAE+∠E=90°．
∵AD是△ABCBC边上的高，
∴∠ADC=90°．
∴∠CAD+∠ACB=90°．
∵∠E=∠ACB，
∴∠BAE=∠CAD．
∵AE是⊙O的直径，
∴∠ABE=90°．
∴∠BAE+∠E=90°．
∵AD是△ABCBC边上的高，
∴∠ADC=90°．
∴∠CAD+∠ACB=90°．
∵∠E=∠ACB，
∴∠BAE=∠CAD．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
