题目内容
如图，BC是直径，AD=DC，∠ADB=20°，∠ACB=______，∠DBC=______．
∵
=
，
∴∠ADB=∠ACB（同弧所对圆周角相等），
∵∠ADB=20°，
∴∠ACB=20°，
∵BC是直径，
∴∠BDC=90°（直径所对圆周角等于90°），
∵AD=DC，
∴
=
，
∴∠DBC=∠DCA（等弧所对圆周角相等），
∵∠ACB=20°，
∵∠BDC=∠DBC+∠DCB=90°，
∴∠DBC+∠DCA=∠DBC+∠DCB-∠ACB=90°-20°=70°，
∴∠DBC=∠DCA=35°．
故答案为：20°，35°．
 |
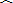| AB |
|
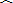| AB |
∴∠ADB=∠ACB（同弧所对圆周角相等），
∵∠ADB=20°，
∴∠ACB=20°，
∵BC是直径，
∴∠BDC=90°（直径所对圆周角等于90°），
∵AD=DC，
∴
|
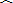| AD |
|
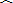| CD |
∴∠DBC=∠DCA（等弧所对圆周角相等），
∵∠ACB=20°，
∵∠BDC=∠DBC+∠DCB=90°，
∴∠DBC+∠DCA=∠DBC+∠DCB-∠ACB=90°-20°=70°，
∴∠DBC=∠DCA=35°．
故答案为：20°，35°．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
