题目内容
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 为
为![]() 上一点,
上一点,![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() ,求
,求![]() 的长.
的长.
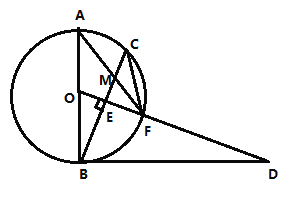
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)欲证明BD是⊙O的切线,只要证明BD⊥AB;
(2)连接AC,证明△FCM∽△FAC即可解决问题;
(3)连接BF,想办法求出BF,FM即可解决问题.
(1)∵![]() ,
,
∴∠AFC=∠ABC,
又∵∠AFC=∠ODB,
∴∠ABC=∠ODB,
∵OE⊥BC,
∴∠BED=90°,
∴∠ODB+∠EBD=90°,
∴∠ABC+∠EBD=90°,
∴OB⊥BD,
∴BD是⊙O的切线;
(2)连接AC,
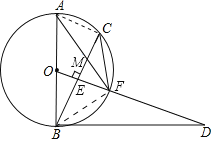
∵OF⊥BC,
∴![]() ,
,![]() ,
,
∴∠BCF=∠FAC,
又∵∠CFM=∠AFC,
∴△FCM∽△FAC,
∴![]() ;
;
(3)连接BF,
∵AB是⊙O的直径,且AB=10,
∴∠AFB=90°,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴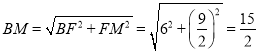 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某中学共有学生2000名,各年级男、女生人数如下表:
年级 | 六年级 | 七年级 | 八年级 | 九年级 |
男生 | 250 | z | 254 | 258 |
女生 | x | 244 | y | 252 |
若从全校学生中任意抽取一名,抽到六年级女生的概率是0.12;若将各年级的男、女学生人数制成扇形统计图,八年级女生对应扇形的圆心角为44.28°.
(1)求x,y,z的值;
(2)求各年级女生的平均数;
(3)如果从八年级随机抽取36名学生参加社会实践活动,求抽到八年级某同学的概率.