题目内容
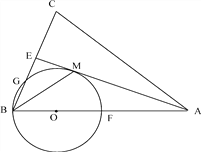
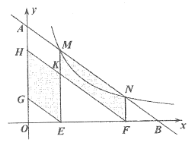
【题目】如图,![]() 是等边三角形,点
是等边三角形,点![]() 在边
在边![]() 上(点
上(点![]() 与点
与点![]() 不重合) ,过点
不重合) ,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,
,![]() 分别为
分别为![]() 的中点,连结
的中点,连结![]() .
.

(1)求证:![]()
(2)![]() 的大小是 .
的大小是 .
【答案】(1)见解析;(2)120°
【解析】
(1)易证△ADE是等边三角形,可求得![]() ,然后利用三角形中位线定理得到
,然后利用三角形中位线定理得到![]() ,
,![]() ,即可证明
,即可证明![]() ;
;
(2)根据三角形中位线定理和三角形外角的性质求出∠MNE=∠ABE,∠ENP=120°-∠ABE,然后根据∠MNP=∠MNE+∠ENP计算即可.
解:(1)∵△ABC是等边三角形,
∴AB=AC,∠ABC=∠ACB=60°,
∵DE∥AB,
∴∠ABC=∠ADE=60°,∠ACB=∠AED=60°,
∴∠ADE=∠AED=60°,
∴△ADE是等边三角形,
∴AD=AE,
∴![]() ,
,
∵M、N分别为DE、BE的中点,
∴![]() ,
,
∵N、P分别为BE、BC的中点,
∴![]() ,
,
∴![]() ;
;
(2)∵M、N、P分别为DE、BE、BC的中点,
∴MN∥AB,NP∥EC,
∴∠MNE=∠ABE,∠BNP=∠BEC=∠A+∠ABE=60°+∠ABE,
∴∠ENP=180°-∠BNP=180°-60°-∠ABE=120°-∠ABE,
∴∠MNP=∠MNE+∠ENP=∠ABE+120°-∠ABE=120°,
故答案为:120°.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目