��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�OΪ����ԭ�㣬������y��a��x+3����x��1����a��0����x�ύ��A��B���㣨��A�ڵ�B����ࣩ��
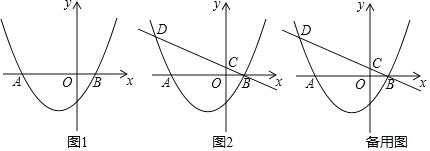
��1�����A���B�����ꣻ
��2����a��![]() ����M����������һ���㣬�������MAO������45�������M�ĺ�����m��ȡֵ��Χ��
����M����������һ���㣬�������MAO������45�������M�ĺ�����m��ȡֵ��Χ��
��3��������B��ֱ��l��y��kx+b��y�������ύ�ڵ�C���������ߵ���һ������Ϊ��D����CD��4BC������P�������߶Գ����ϣ���Q���������ϣ��Ե�B��D��P��QΪ������ı����ܷ��Ϊ���Σ����ܣ������P�����ꣻ�����ܣ���˵�����ɣ�
���𰸡���1��A����3��0����B��1��0������2��M��4��7������2��m��4����3����P������ΪP����1��4����1��![]() ����
����
��������
��1��y��a��x+3����x��1��,��y��0,��x��1��3,�������;
��2���֡�MAO=45��,��M��AO=45���������,�ֱ���⼴��;
��3���ֵ�BD�Ǿ��εı�, BD�Ǿ��εı��������,�ֱ���⼴�ɣ�
��1��y��a��x+3����x��1��,��y��0,��x��1��3,
�ʵ�A��B������ֱ�Ϊ������3��0��,��1��0��;
��2�������ߵı���ʽΪ:y��![]() ��x+3����x��1����,
��x+3����x��1����,
����MAO��45��ʱ,��ͼ��ʾ,��ֱ��AM�ı���ʽΪ:y��x��,
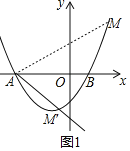
�����٢ڲ����:m��x��4��3����ȥ��3��,�ʵ�M��4,7��;
�ڡ�M��AO��45��ʱ,
ͬ���ɵ�:��M����2,��1��;
��:��2��m��4;
��3���ٵ�BD�Ǿ��εĶԽ���ʱ,��ͼ2��ʾ,
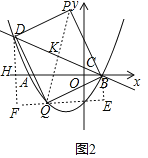
����Q��x���ƽ����EF,����B��BE��EF,����D��DF��EF,
�����ߵı���ʽΪ:y��ax2+2ax��3a,�����ĶԳ���Ϊ:x��1,
�����ߵ�A��B������ֱ�Ϊ:����3,0������1��0��,���P�ĺ�����Ϊ:1,OB��1,
��CD��4BC,���D�ĺ�����Ϊ����4,�ʵ�D����4,5a��,��HD��5a,
�߶�BD���е�K�ĺ�����Ϊ:![]() ,���Q�ĺ�����Ϊ:��2,
,���Q�ĺ�����Ϊ:��2,
���Q����2,��3a��,��HF��BE��3a,
�ߡ�DQF+��BQE��90��,��BQE+��QBE��90��,
���QBE����DQF,
���DFQ�ס�QEB,��![]() ,
,![]() ,���:a��
,���:a��![]() ����ȥ��ֵ��,
����ȥ��ֵ��,
ͬ����PGB�ա�DFQ��AAS��,
��PG��DF��8a��4,�ʵ�P����1,4��;
����ͼ3,��BD�Ǿ��εı�ʱ,
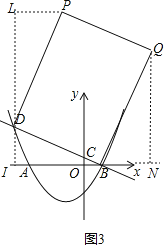
��DI��x��,QN��x��,����P��PL��DI�ڵ�L,
ͬ����PLD�ա�BNQ��AAS��,
��BN��PL��3,
���Q�ĺ�����Ϊ4,���Q��4,21a��,
��QN��DL��21a,ͬ����PLD�ס�DIB,
��![]() ,��
,��![]() ,���:a��
,���:a��![]() ����ȥ��ֵ����
����ȥ��ֵ����
LI��26a��![]() ,�ʵ�P����1,
,�ʵ�P����1, ![]() ��;
��;
����,��P������Ϊ:P����1,4����1, ![]() ����
����