题目内容
【题目】抛物线M：y=ax2-4ax+a-1（a≠0）与x轴交于A，B两点（点A在点B左侧），抛物线的顶点为D．
（1）抛物线M的对称轴是直线______；
（2）当AB=2时，求抛物线M的函数表达式；
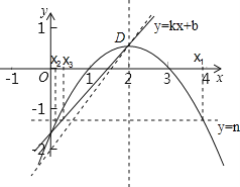
（3）在（2）的条件下，直线l：y=kx+b（k≠0）经过抛物线的顶点D，直线y=n与抛物线M有两个公共点，它们的横坐标分别记为x1，x2，直线y=n与直线l的交点的横坐标记为x3（x3＞0），若当-2≤n≤-1时，总有x1-x3＞x3-x2＞0，请结合函数的图象，直接写出k的取值范围．
【答案】（1）x=2；（2）y=-
x2+2x-
；（3）k＞
【解析】
（1）根据抛物线解析式，即可得出其对称轴所在直线；
（2）根据抛物线的对称轴得出A、B两点坐标，代入抛物线解析式求解，即可得出其解析式；
（3）首先将抛物线化为顶点式，得出点D坐标，然后根据直线与抛物线的交点坐标结合函数图象，即可判定k的取值范围.
（1）∵抛物线M的表达式为y=ax2-4ax+a-1，
∴抛物线M的对称轴为直线x=-
=2．
故答案为：x=2．
（2）∵抛物线y=ax2-4ax+a-1的对称轴为直线x=2，抛物线M与x轴的交点为点A、B（点A在点B左侧），AB=2，
∴点A的坐标为（1，0），点B的坐标为（3，0）．
将A（1，0）代入y=ax2-4ax+a-1，得：a-4a+a-1=0，
解得：a=-，
∴抛物线M的函数表达式为y=-x2+2x-．
（3）∵y=-x2+2x-=-（x-2）2+，
∴点D的坐标为（2，）．
∵直线y=n与直线l的交点的横坐标记为x3（x3＞0），且当-2≤n≤-1时，总有x1-x3＞x3-x2＞0，
∴直线l与y轴的交点在（0，-2）下方，
∴b＜-2．
∵直线l：y=kx+b（k≠0）经过抛物线的顶点D，
∴2k+b=，
∴k=
-
＞．
