Question

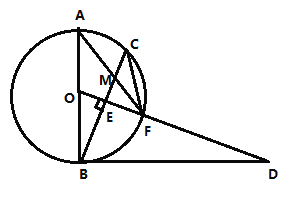
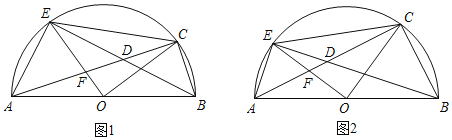
【题目】如图，AB是半圆O的直径，C为半圆弧上一点，在AC上取一点D，使BC=CD，连结BD并延长交⊙O于E，连结AE，OE交AC于F．

(1)求证：△AED是等腰直角三角形；

(2)如图1，已知⊙O的半径为．

①求的长；

②若D为EB中点，求BC的长．

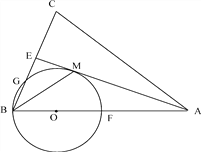
(3)如图2，若AF：FD=7：3，且BC=4，求⊙O的半径．

Answer 1

【答案】(1)见解析；(2)①；②；(3)

【解析】

（1）由已知可得△BCD是等腰直角三角形，所以∠CBD＝∠EAD＝45°，因为∠AEB＝90°可证△AED是等腰直角三角形；

（2）①已知可得∠EAD＝45°，∠EOC＝90°，则△EOC是等腰直角三角形，所以CE的弧长=×2×π×=；

②由已知可得ED＝BD，在Rt△ABE中，(2)2=AE2+(2AE)2，所以AE＝2，AD＝2，易证△AED∽△BCD，所以BC＝；

（3）由已知可得AF＝AD，过点E作EG⊥AD于G，EG=AD，GF=AD，tan∠EFG=，得出FO=r，在Rt△COF中，FC=r，EF=r，在Rr△EFG中，由勾股定理，求出AD=r，AF=r，所以AC=AF+FC=，CD=BC=4，AC=4+AD，可得r=4+r，解出r即可．

解：(1)∵BC=CD，AB是直径，

∴△BCD是等腰直角三角形，

∴∠CBD=45°，

∵∠CBD=∠EAD=45°，

∵∠AEB=90°，

∴△AED是等腰直角三角形；

(2)①∵∠EAD=45°，

∴∠EOC=90°，

∴△EOC是等腰直角三角形，

∵⊙O的半径为，

∴CE的弧长=×2×π×=，

故答案为：；

②∵D为EB中点，

∴ED=BD，

∵AE=ED，

在Rt△ABE中，(2)2=AE2+(2AE)2，

∴AE=2，

∴AD=2，

∵ED=AE，CD=BC，∠AED=∠BCD=90°，

∴△AED∽△BCD，

∴BC=，

故答案为：；

(3)∵AF：FD=7：3，

∴AF=AD，

过点E作EG⊥AD于G，

∴EG=AD，

∴GF=AD，

∴tan∠EFG=，

∴==，

∴FO=r，

在Rt△COF中，FC=r，

∴EF=r，

在Rt△EFG中，(r)2=(AD)2+(AD)2，

∴AD=r，

∴AF=r，

∴AC=AF+FC=r，

∵CD=BC=4，

∴AC=4+AD=4+r，

∴r=4+r，

∴r=，

故答案为：．