题目内容
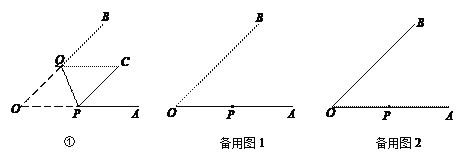
【题目】把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4 cm,则球的半径长是( )

A. 2cm B. 2.5cm C. 3cm D. 4cm
【答案】B
【解析】分析:首先由题意,⊙O与BC相切,记切点为G,作直线OG,分别交AD、劣弧EF于点H、I,再连接OF,易求得FH的长,然后设求半径为r,则OH=4-r,然后在Rt△OFH中,r2-(4-r)2=22,解此方程即可求得答案.
详解:
由题意,⊙O与BC相切,记切点为G,作直线OG,分别交AD、劣弧EF于点H、I,再连接OF,
在矩形ABCD中,AD∥BC,而IG⊥BC,
∴IG⊥AD,
∴在⊙O中,FH=![]() EF=2,
EF=2,
设求半径为r,则OH=4-r,
在Rt△OFH中,r2-(4-r)2=22,
解得r=2.5,
∴这个球的半径是2.5厘米.
故选B.

练习册系列答案
相关题目