题目内容
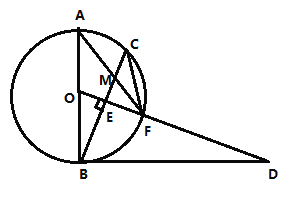
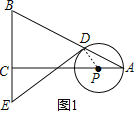
【题目】如图Rt△ABC中,∠ACB=90°,AC=4,BC=2,点P在边AC上运动(点P与点A、C不重合).以P为圆心,PA为半径作⊙P交边AB于点D、过点D作⊙P的切线交射线BC于点E(点E与点B不重合).
(1)求证:BE=DE;
(2)若PA=1.求BE的长;
(3)在P点的运动过程中.(BE+PA)PA的值是否有最大值?如果有,求出最大值;如果没有,请说明理由.

【答案】(1)证明见解析;(2)BE=3;(3)(BE+PA)PA有最大值,最大值为![]() .
.
【解析】
(1)由半径相等可设∠PAD=∠ADP=α,根据切线的性质得到∠EDP=90°,证明∠BDE=90°-α,由∠ACB=90°,得到∠B=90°﹣α,再根据“等角对等边”即可求解;
(2)过点E作EG⊥BD,则点G为BD的中点,根据等量代换得到∠GED=∠BAC,从而求出tan∠BAC![]() ,则cos∠BAC
,则cos∠BAC ![]() ,sin∠BAC
,sin∠BAC ![]() ,根据锐角三角函数的定义即可求出AD,DG以及BE;
,根据锐角三角函数的定义即可求出AD,DG以及BE;
(3)设PA=x,根据(2)可得出(BE+PA)PA=﹣2x2+5x,根据二次函数的性质即可求解.
解:(1)连接PD,∵PA=PD,
∴设∠PAD=∠ADP=α,
∵DE是圆的切线,则∠EDP=90°,
∴∠PDA+∠BDE=90°,即α+∠BDE=90°,
∴∠BDE=90°-α
∵∠ACB=90°,
∴∠B=90°﹣α,
∴∠BDE=∠B
∴BE=DE;
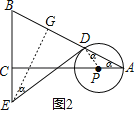
(2)过点E作EG⊥BD,则点G为BD的中点,
∵∠GED+∠EDB=90°,∠PDA+∠EDB=90°,
∴∠GED=∠PDA,
∴∠GED=∠BAC,
tan∠BAC![]() ,则cos∠BAC
,则cos∠BAC ![]() ,sin∠BAC
,sin∠BAC ![]() ,
,
∵PA=1,AC=4,BC=2,
∴AB=![]() ,
,
∴AD=2PAcos∠BAC ![]() ,
,
DG=BG![]() BD=(AB﹣AD)
BD=(AB﹣AD)![]() (2
(2![]() )
)![]() ,
,
BE=DE![]() 3,
3,
(3)设PA=x,
由(2)知:BE=DE=5﹣
则(BE+PA)PA=(5﹣2x+x)x=﹣x2+5x,
∵﹣1<0,故(BE+PA)PA有最大值,
∴当x![]() 时,有最大值为
时,有最大值为![]() .
.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案