题目内容
【题目】请阅读下列材料,并完成相应的任务.
在数学中,当问题的条件不够时间,常添加辅助线构成新图形,形成新关系,建立已知与未知的桥梁,从而把原问题转化为易于解决的问题.在著名美籍匈牙利数学教波利亚所著的《数学的发现》一书中有这样一个例子:试作一个三角形,使它的三边长分别是各条中线长的三分之一,解决这个问题的步骤如下:

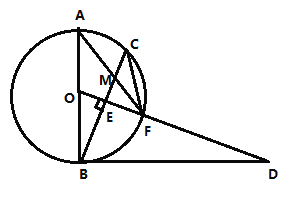
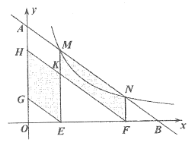
第一步,如图1,己知![]() 的三条中线
的三条中线![]() ,
,![]() 和
和![]() 相交于点
相交于点![]() ,则有
,则有![]() .
.
下面是该结论的部分证明过程:

证明:如图1,过点![]() 作
作![]() 的平分线,交
的平分线,交![]() 的延长线于点
的延长线于点![]() ,则
,则![]() .
.
又![]() ,
,
∴![]() .
.
∴![]() .
.
∵点![]() 是
是![]() 的中点,
的中点,
∴![]() .
.
……
第二步,同理可以证明:![]() .
.
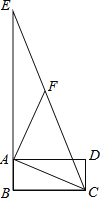
第三步,如图2,取BM的中点![]() ,连接
,连接![]() .则
.则![]() 的三边长分别是各条中线长的三分之一.
的三边长分别是各条中线长的三分之一.
任务:(1)请在上面第一步中证明过程的基础上完成对结论![]() 的证明;
的证明;
(2)请完成第三步的结论的证明;
(3)请直接写出图2中![]() 与
与![]() 的面积比:
的面积比:![]() _______.
_______.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)证明![]() 即可得到BM=GC,再由
即可得到BM=GC,再由![]() 即可解答;
即可解答;
(2)根据![]() 得出
得出![]() ,再得出
,再得出![]() ,根据中位线的性质得出
,根据中位线的性质得出![]() ,进而得到
,进而得到![]() 即可;
即可;
(3)根据三角形中线将三角形的面积平分即可推出.
(1)解:∵![]() ,
,
∴![]() .
.
∵![]() 是
是![]() 边上的中线,
边上的中线,
∴![]() .
.
在![]() 和
和![]() 中,
中,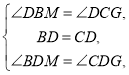
∴![]() (ASA),
(ASA),
∴BM=GC,
∴![]() .
.
(2)证明:∵![]() ,
,
∴![]() .
.
∵![]() 是
是![]() 的中点,
的中点,
∴![]()
∵![]() ,
,
∴![]()
∵![]() 是
是![]() 的中点,
的中点,
∴![]() 是
是![]() 的中位线,
的中位线,
则![]() ,又
,又![]() ,
,
∴![]() .
.
则![]() 的三边长分别是各条中线长的三分之一.
的三边长分别是各条中线长的三分之一.
(3)∵Q是BM 的中点,
∴S△BMD=2S△QMD,
∵AM=2MD
∴S△ABM=2S△BMD
∴S△ABD=3S△BMD=6S△QMD,
∵点D是BC中点,
∴S△ABC=2S△ABD=12 S△QMD,
故![]() ,
,
故答案为:![]() .
.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目