题目内容
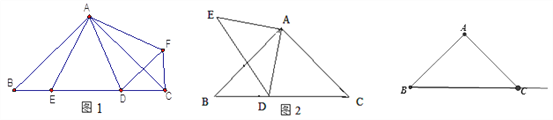
【题目】如图,点A为平面直角坐标系第一象限内一点,直线y=x过点A,过点A作AD⊥y轴于点D,点B是y轴正半轴上一动点,连接AB,过点A作AC⊥AB交x轴于点C.
(1)如图,当点B在线段OD上时,求证:AB=AC;
(2)①如图,当点B在OD延长线上,且点C在x轴正半轴上, OA、OB、OC之间的数量关系为________(不用说明理由);
②当点B在OD延长线上,且点C在x轴负半轴上,写出OA、OB、OC之间的数量关系,并说明原因.
(3)直线BC分别与直线AD、直线y=x交于点E、F,若BE=5,CF=12,直接写出AB的长.

【答案】(1)证明见解析;(2)①OA=![]() (OC+OB);②OA=
(OC+OB);②OA=![]() (OB-OC);(3)10
(OB-OC);(3)10![]() ; 15
; 15![]() .
.
【解析】
(1)过点A作AE⊥OC于点E,先证明四边形ADOE是正方形,再证明Rt△ADB≌Rt△AEC(AAS),从而求得结论;(2)①过点A作AE⊥OC于点E,方法同(1)证明四边形ADOE是正方形,Rt△ADB≌Rt△AEC,△AOD是等腰直角三角形,再应用勾股定理即可得结论OA=![]() (OC+OB);②方法同①得结论:OA=
(OC+OB);②方法同①得结论:OA=![]() (OB-OC);(3)①当点B在线段OD上时,将△AFC绕点A顺时针旋转90°,AC与AB重合,变为△ABF′,连接EF′,证明∠EBF′=90°,由勾股定理得EF′=13,再证明△AEF≌△AEF′,所以EF= EF′=13,BF=EF-EB=13-5=8,BC=BF+FC=8+12=20,而△ABC是等腰直角三角形,所以AB=
(OB-OC);(3)①当点B在线段OD上时,将△AFC绕点A顺时针旋转90°,AC与AB重合,变为△ABF′,连接EF′,证明∠EBF′=90°,由勾股定理得EF′=13,再证明△AEF≌△AEF′,所以EF= EF′=13,BF=EF-EB=13-5=8,BC=BF+FC=8+12=20,而△ABC是等腰直角三角形,所以AB=![]() =10
=10![]() ; ②当点B在OD延长线上,且点C在x轴正半轴上时,方法同①,解得:AB=15
; ②当点B在OD延长线上,且点C在x轴正半轴上时,方法同①,解得:AB=15![]() ;③当点B在OD延长线上,且点C在x轴负半轴上时,方法同上,解得:AB=3
;③当点B在OD延长线上,且点C在x轴负半轴上时,方法同上,解得:AB=3![]() .
.
(1)过点A作AE⊥OC于点E,
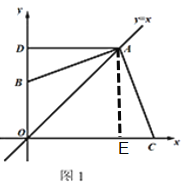
∵AD⊥y,点A在y=x上,∠DOE=90°
∴四边形ADOE是矩形,AE=OE,
∴矩形ADOE是正方形,
∴AD=AE,∠DAE=∠BAC=90°,
∴∠DAB=∠EAC,
又∵∠BDA=∠CEA=90°
∴Rt△ADB≌Rt△AEC
∴AB=AC.
(2)① 过点A作AE⊥OC于点E,
方法同(1)得,四边形ADOE是正方形,Rt△ADB≌Rt△AEC,AB=AC,BD=CE,
∴OC+OB=OC+OD+BD=OC+OD+CE=OE+OD=2OD,即OD=![]() (OC+OB)
(OC+OB)
又∵△AOD是等腰直角三角形,
∴由勾股定理得:OA=![]() OD =
OD =![]() ×
×![]() (OC+OB)=
(OC+OB)=![]() (OC+OB),
(OC+OB),
即OA=![]() (OC+OB),
(OC+OB),
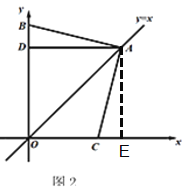
②过点A作AE⊥OC于点E,
方法同(1)得,四边形ADOE是正方形,Rt△ADB≌Rt△AEC,AB=AC,BD=CE,
∴OB-OD=OC+OE,即OB-OC=OD+OE=2OD=![]() OA,
OA,
又∵△AOD是等腰直角三角形,
∴由勾股定理得:OA=![]() OD,OD=
OD,OD= ![]() OA ,
OA ,
∴OB-OC= OD+OE=2OD=![]() OA,即OB-OC=
OA,即OB-OC=![]() OA,OA=
OA,OA=![]() (OB-OC)
(OB-OC)
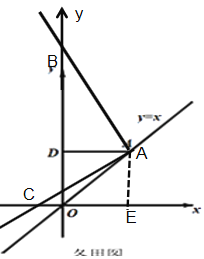
(3)①当点B在线段OD上时,
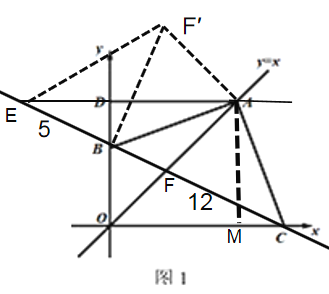
将△AFC绕点A顺时针旋转90°,AC与AB重合,变为△ABF′,连接EF′,BF′=CF=12,∠ACB=∠ABC=∠ABF′=45°,∠CBF′=∠ABC+∠ABF′=90°,所以∠EBF′=90°,
又∵BE=5,∴EF′=13,
∵∠F′AO=90°, ∠FAE=∠F′AE=45°,AE=AE,AF=AF′,
∴△AEF≌△AEF′
∴EF= EF′=13,BF=EF-EB=13-5=8,BC=BF+FC=8+12=20,
由(1)得:△ABC是等腰直角三角形,∴AB=![]() =10
=10![]() ;
;
②当点B在OD延长线上,且点C在x轴正半轴上时,
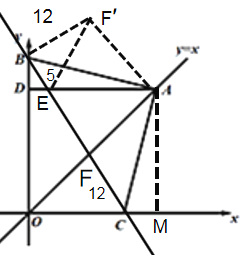
方法同①,旋转△AFC到△AF′B,证出∠EBF′,EF′=13=EF,BC=BE+EF+FC=5+13+12=30,所以等腰直角三角形ABC的直角边AB=15![]() ;
;
③当点B在OD延长线上,且点C在x轴负半轴上,
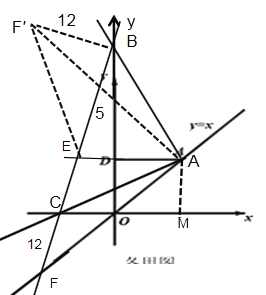
已证△ABC是等腰直角三角形,
过点B作BF′⊥BC于点B,截取 BF′=CF=12, 连接F′E、F′A,∵BE=5,
∴∠ABF′=∠ACF=135°,EF′=13
AB=AC,
∴△ABF′≌△ACF,可得AF′=AF,∠/span>BAF′=∠CAF,
∴∠BAC=∠F′AF=90°,
∵∠EAF=45°,
∴∠EAF=45°=∠EAF′,又AE=AE
∴△EAF≌△EAF′,
∴EF=EF′=13,EC=EF-CF=13-12=1,BC=BE+EC=1+5=6,
∴在等腰直角三角形ABC中,直角边AB=3![]() .
.

【题目】为响应国家节能减排的号召,鼓励居民节约用电,各省市先后出台了“阶梯价格”制度,如表中是某市的电价标准(每月)
阶梯 | 电量x(单位:度) | 电费价格(单位:元/度) |
一档 | 0<x≤180 | a |
二档 | 180<x≤400 | b |
三档 | x>400 | 0.95 |
(1)已知陈女士家三月份用电256度,缴纳电费154.56元,四月份用电318度,缴纳电费195.48元请你根据以上数据,求出表格中的a,b的值.
(2)5月份开始用电增多,陈女士缴纳电费280元,求陈女士家5月份的用电量.
【题目】为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶![]() 次,为了比较两人的成绩,制作了如下统计图表:
次,为了比较两人的成绩,制作了如下统计图表:
甲乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中 | |
甲 |
|
| ||
乙 |
|
|
|
甲乙射击成绩折线图
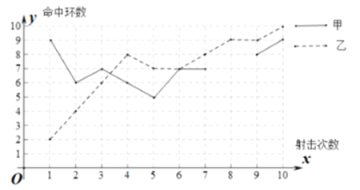
(1)请补全上述图表(请直接在统计表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,则_____胜出,理由是____________________;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?说明理由.