题目内容
【题目】为了从甲、乙两名选手中选拔一个参加射击比赛，现对他们进行一次测验，两个人在相同条件下各射靶
次，为了比较两人的成绩，制作了如下统计图表：
甲乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中 | |
甲 |
|
| ||
乙 |
|
|
|
甲乙射击成绩折线图
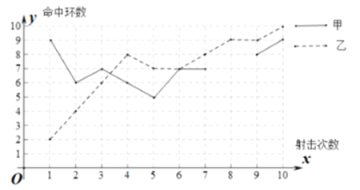
（1）请补全上述图表（请直接在统计表中填空和补全折线图）；
（2）如果规定成绩较稳定者胜出，则_____胜出，理由是____________________；
（3）如果希望（2）中的另一名选手胜出，根据图表中的信息，应该制定怎样的评判规则？说明理由．
【答案】（1）补全图表见解析；（2）甲，理由见解析；（3）可制定评判规则为：命中10环次数较多者胜出，理由见解析．
【解析】
（1）根据甲选手成绩的平均数可求出甲选手第8次命中的环数，即可补全折线图；然后根据平均数、中位数和方差的求法补全统计表；
（2）根据方差的意义可得答案；
（3）可根据乙选手命中
环1次，甲选手没有命中环来制定评判规则．
解：（1）甲选手第8次命中的环数为：7×10－（9＋6＋7+6＋5＋7＋7＋8＋9）＝6，
将甲选手的成绩从小到大排列为：5，6，6，6，7，7，7，8，9，9，
中间两次的环数分别为：7，7，故中位数为
，
，
乙选手成绩的平均数为：
，
补全表格和折线图为：
平均数 | 中位数 | 方差 | 命中 | |
甲 |
| 7 | 1.6 |
|
乙 | 7 |
|
|
|
（2）如果规定成绩较稳定者胜出，则甲胜出，
理由：因为甲的方差小于乙的方差，
所以甲的成绩比乙稳定，即甲胜出；
（3）可制定评判规则为：命中10环次数较多者胜出，
理由：因为乙选手命中环1次，甲选手没有命中环，
所以乙胜出．
【题目】大成蔬菜公司以
元
千克的成本价购进
番茄，公司想知道番茄的损坏率，从所有随机抽取若干进行统计，部分结果如表：
番茄总质量 |
|
|
|
|
|
|
损坏番茄质量 |
|
|
|
|
|
|
番茄损坏的频率 |
|
|
|
|
|
|
估计这批番茄损坏的概率为______（精确到
），据此，若公司希望这批番茄能获得利润
元，则销售时（去掉损坏的番茄）售价应至少定为______元/千克．
