题目内容
【题目】如图，在△ABC中，AB=AC=4，∠BAC=120°，AD为BC边上的高，点P从点B以每秒
个单位长度的速度向终点C运动，同时点Q从点C以每秒1个单位长度的速度向终点A运动，其中一个点到达终点时，两点同时停止.
(1)求BC的长；
(2)设△PDQ的面积为S，点P的运动时间为t秒，求S与t的函数关系式，并写出自变量的取值范围；
(3)在动点P、Q的运动过程中，是否存在PD=PQ，若存在，求出△PDQ的周长，若不存在，请说明理由.
【答案】(1) 4
;(2)①S△PDQ=-
t2+
t(0≤t≤2);②S△PDQ=t -t2 (2<t≤4);（3）存在PD=PQ，此时△PDQ的周长为3.
【解析】
(1)根据等腰三角形性质三线合一和含30°锐角的直角三角形的性质即可解答；（2）分当点P在线段BD上运动和当点P在线段DC上运动，过点Q作QM⊥BC于点M，用含时间t的代数式分别表示出PD=BD-BP=2-t或者PD= BP - BD =t- 2，、QM 
CQ=t的长，根据三角形面积公式即可求解；（3）根据题意可得，当PD=PQ时，PD=PQ，
用含t的式子分别表示出Rt△PMQ的三边，由勾股定理得QM2+MP2=QP2，解得t=3后得到△DPQ是等边三角形，边长为，从而求出周长.
解：（1）△ABC中，∵AB=AC=4，∠BAC=120°，AD⊥ BC，
∴∠B=∠C=30°，BD=DC
∴AD=AB=2，由勾股定理得：BD=DC= 2
∴BC=2BD=4;
（2）过点Q作QM⊥BC于点M，
∵CQ=t，∠C=30°，BP=t
∴QM= CQ=t ，
①当点P在线段BD上运动时，即0≤t≤2，如图：
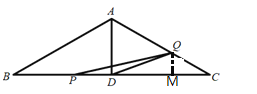
PD=BD-BP=2-t
∴S△PDQ=×PD×QM=×（2-t）×t=-t2+t(0≤t≤2);
②当点P在线段DC上运动时，即2<t≤4，如图：
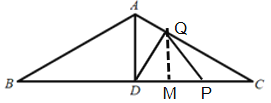
PD= BP - BD =t- 2，方法同①得：
S△PDQ=×PD×QM=×（t -2）×t=t -t2 (2<t≤4);
（3）当点P在BD上运动时，∠BDQ>90°，PD≠PQ，所以若PD=PQ=t -2 ，则PD=PQ如（2）②中图形，此时PD=PQ=t- 2，PC=BC-BP=4-t，MC=
=t ，MP=MC-PC=t-(4-t)=
t-4，
Rt△PMQ中，∵QM2+MP2=QP2
∴（t）2+（t-4）2=（t -2）2，
化简得：t2-6t+9=0，即（t-3）2=9，∵t >0
解得t=3，即PD=PQ=t -2=3 -2==PC，
又∵∠C=30°，∴∠C=∠PQC=30°，∠DPQ=∠C+∠PQC=60°，即△DPQ是等边三角形，
∴△DPQ的周长=3PD=3.
