题目内容
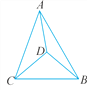
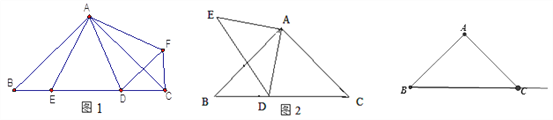
【题目】(1)如图1,在Rt△ABC 中, ![]() ,D、E是斜边BC上两动点,且∠DAE=45°,将△
,D、E是斜边BC上两动点,且∠DAE=45°,将△![]() 绕点
绕点![]() 逆时针旋转90后,得到△
逆时针旋转90后,得到△![]() ,连接
,连接![]() .
.
(1)试说明:△![]() ≌△
≌△![]() ;
;
(2)当BE=3,CE=9时,求∠BCF的度数和DE的长;
(3)如图2,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,D是斜边BC所在直线上一点,BD=3,BC=8,求DE2的长.
【答案】(1)略(2)∠BCF=90° DE=5 (3)34或130
【解析】试题分析: ![]() 由
由![]() 得到
得到![]()
![]()
![]()
![]()
![]() 即
即![]()
![]() 从而得到
从而得到![]()
![]() 由△
由△![]() 得到
得到![]() ,再证明
,再证明![]() 利用勾股定理即可得出结论.
利用勾股定理即可得出结论.
![]() 过点
过点![]() 作
作![]() 于
于![]() ,根据等腰三角形三线合一得,
,根据等腰三角形三线合一得, ![]()
![]() 或
或![]() 求出
求出![]() 的长,即可求得
的长,即可求得![]() .
.
试题解析: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
即![]()
在![]() 和
和![]() 中,
中, 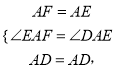
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
设![]()
![]()
![]()
![]()
![]()
解得: ![]()
故![]()
![]() 过点
过点![]() 作
作![]() 于
于![]() ,根据等腰三角形三线合一得,
,根据等腰三角形三线合一得,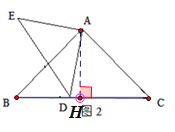
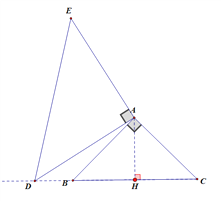
![]()
![]() 或
或![]()
![]() 或
或![]()
![]() 或
或![]()

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目