题目内容
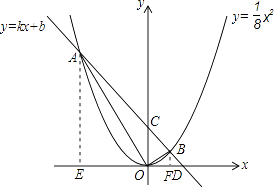
【题目】如图,直线y=kx+b(b>0)与抛物线 ![]() 相交于点A(x1 , y1),B(x2 , y2)两点,与x轴正半轴相交于点D,与y轴相交于点C,设△OCD的面积为S,且kS+32=0.
相交于点A(x1 , y1),B(x2 , y2)两点,与x轴正半轴相交于点D,与y轴相交于点C,设△OCD的面积为S,且kS+32=0.
(1)求b的值;
(2)求证:点(y1 , y2)在反比例函数 ![]() 的图象上;
的图象上;
(3)求证:x1OB+y2OA=0.
【答案】
(1)
解:∵直线y=kx+b(b>0)与x轴正半轴相交于点D,与y轴相交于点C,
∴令x=0,得y=b;令y=0,x=﹣ ![]() ,
,
∴△OCD的面积S= ![]() (﹣
(﹣ ![]() )b=﹣
)b=﹣ ![]() .
.
∵kS+32=0,
∴k(﹣ ![]() )+32=0,
)+32=0,
解得b=±8,
∵b>0,
∴b=8;
(2)
证明:由(1)知,直线的解析式为y=kx+8,即x= ![]() ,
,
将x= ![]() 代入y=
代入y= ![]() x2,得y=
x2,得y= ![]() (
( ![]() )2,
)2,
整理,得y2﹣(16+8k2)y+64=0.
∵直线y=kx+8与抛物线 ![]() 相交于点A(x1,y1),B(x2,y2)两点,
相交于点A(x1,y1),B(x2,y2)两点,
∴y1,y2是方程y2﹣(16+8k2)y+64=0的两个根,
∴y1y2=64,
∴点(y1,y2)在反比例函数 ![]() 的图象上
的图象上
(3)
方法一:
证明:由勾股定理,得
OA2= ![]() +
+ ![]() ,OB2=
,OB2= ![]() +
+ ![]() ,AB2=(x1﹣x2)2+(y1﹣y2)2,
,AB2=(x1﹣x2)2+(y1﹣y2)2,
由(2)得y1y2=64,
同理,将y=kx+8代入y= ![]() x2,
x2,
得kx+8= ![]() x2,即x2﹣8kx﹣64=0,
x2,即x2﹣8kx﹣64=0,
∴x1x2=﹣64,
∴AB2= ![]() +
+ ![]() +
+ ![]() +
+ ![]() ﹣2x1x2﹣2y1y2=
﹣2x1x2﹣2y1y2= ![]() +
+ ![]() +
+ ![]() +
+ ![]() ,
,
又∵OA2+OB2= ![]() +
+ ![]() +
+ ![]() +
+ ![]() ,
,
∴OA2+OB2=AB2,
∴△OAB是直角三角形,∠AOB=90°.
如图,过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F.
∵∠AOB=90°,
∴∠AOE=90°﹣∠BOF=∠OBF,
又∵∠AEO=∠OFB=90°,
∴△AEO∽△OFB,
∴ ![]() =
= ![]() ,
,
∵OE=﹣x1,BF=y2,
∴ ![]() =
= ![]() ,
,
∴x1OB+y2OA=0.
方法二:
分别过A,B两点作x轴垂线,垂足分别为E、F,
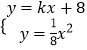 x2﹣8kx﹣64=0,
x2﹣8kx﹣64=0,
∴x1=4k﹣4 ![]() ,x2=4k+
,x2=4k+ ![]() ,
,
y1=4k2+8﹣4k ![]() ,y2=4k2+8+
,y2=4k2+8+ ![]() ,
,
∴A(4k﹣4 ![]() ,4k2+8﹣4k
,4k2+8﹣4k ![]() ),
),
B(4k+ ![]() ,4k2+8+
,4k2+8+ ![]() ),
),
KOA×KOB= ![]() =
= ![]() =﹣1<
=﹣1<
∴OA⊥OB,∠AOE+∠BOF=90°,AE⊥x轴,∠AOE+∠OAE=90°,
∴∠BOF=∠OAE,
∵BF⊥x轴,∴∠AEO=∠BFO=90°,
∴△AEO∽△BFO,
∴ ![]() ,
,
∵OE=﹣x1,BF=y2,
∴x1OB+y2OA=0.
【解析】(1)先求出直线y=kx+b与x轴正半轴交点D的坐标及与y轴交点C的坐标,得到△OCD的面积S=﹣ ![]() ,再根据kS+32=0,及b>0即可求出b的值;(2)先由y=kx+8,得x=
,再根据kS+32=0,及b>0即可求出b的值;(2)先由y=kx+8,得x= ![]() ,再将x=
,再将x= ![]() 代入y=
代入y= ![]() x2 , 整理得y2﹣(16+8k2)y+64=0,然后由已知条件直线y=kx+8与抛物线
x2 , 整理得y2﹣(16+8k2)y+64=0,然后由已知条件直线y=kx+8与抛物线 ![]() 相交于点A(x1 , y1),B(x2 , y2)两点,知y1 , y2是方程y2﹣(16+8k2)y+64=0的两个根,根据一元二次方程根与系数的关系得到y1y2=64,即点(y1 , y2)在反比例函数
相交于点A(x1 , y1),B(x2 , y2)两点,知y1 , y2是方程y2﹣(16+8k2)y+64=0的两个根,根据一元二次方程根与系数的关系得到y1y2=64,即点(y1 , y2)在反比例函数 ![]() 的图象上;(3)先由勾股定理,得出OA2=
的图象上;(3)先由勾股定理,得出OA2= ![]() +
+ ![]() ,OB2=
,OB2= ![]() +
+ ![]() ,AB2=(x1﹣x2)2+(y1﹣y2)2 , 由(2)得y1y2=64,又易得x1x2=﹣64,则OA2+OB2=AB2 , 根据勾股定理的逆定理得出∠AOB=90°.再过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,根据两角对应相等的两三角形相似证明△AEO∽△OFB,由相似三角形对应边成比例得到
,AB2=(x1﹣x2)2+(y1﹣y2)2 , 由(2)得y1y2=64,又易得x1x2=﹣64,则OA2+OB2=AB2 , 根据勾股定理的逆定理得出∠AOB=90°.再过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,根据两角对应相等的两三角形相似证明△AEO∽△OFB,由相似三角形对应边成比例得到 ![]() =
= ![]() ,即可证明x1OB+y2OA=0.
,即可证明x1OB+y2OA=0.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

【题目】在不透明的袋子中有四张标着数字1,2,3,4的卡片,小明、小华两人按照各自的规则玩抽卡片游戏. 小明画出树状图如图所示:
小华列出表格如下:
第一次 | 1 | 2 | 3 | 4 |
1 | (1,1) | (2,1) | (3,1) | (4,1) |
2 | (1,2) | (2,2) | ① | (4,2) |
3 | (1,3) | (2,3) | (3,3) | (4,3) |
4 | (1,4) | (2,4) | (3,4) | (4,4) |
回答下列问题:
(1)根据小明画出的树形图分析,他的游戏规则是,随机抽出一张卡片后(填“放回”或“不放回”),再随机抽出一张卡片;
(2)根据小华的游戏规则,表格中①表示的有序数对为;
(3)规定两次抽到的数字之和为奇数的获胜,你认为谁获胜的可能性大?为什么?