Question

【题目】已知：关于x的二次函数y=﹣x2+ax（a＞0），点A（n，y1）、B（n+1，y2）、C（n+2，y3）都在这个二次函数的图象上，其中n为正整数．
（1）y1=y2 ， 请说明a必为奇数；
（2）设a=11，求使y1≤y2≤y3成立的所有n的值；
（3）对于给定的正实数a，是否存在n，使△ABC是以AC为底边的等腰三角形？如果存在，求n的值（用含a的代数式表示）；如果不存在，请说明理由．

Answer 1

【答案】
（1）

解：∵点A（n，y1）、B（n+1，y2）、C（n+2，y3）都在二次函数y=﹣x2+ax（a＞0）的图象上，

∴y1=﹣n2+an，y2=﹣（n+1）2+a（n+1）

∵y1=y2，

∴﹣n2+an=﹣（n+1）2+a（n+1）

整理得：a=2n+1

∴a必为奇数

（2）

解：当a=11时，∵y1≤y2≤y3

∴﹣n2+11n≤﹣（n+1）2+11（n+1）≤﹣（n+2）2+11（n+2）

化简得：0≤10﹣2n≤18﹣4n，

解得：n≤4，

∵n为正整数，

∴n=1、2、3、4

（3）

解：假设存在，则BA=BC，如右图所示．

过点B作BN⊥x轴于点N，过点A作AD⊥BN于点D，CE⊥BN于点E．

∵xA=n，xB=n+1，xC=n+2，

∴AD=CE=1．

在Rt△ABD与Rt△CBE中，

，

∴Rt△ABD≌Rt△CBE（HL）．

∴∠ABD=∠CBE，即BN为顶角的平分线．

由等腰三角形性质可知，点A、C关于BN对称，

∴BN为抛物线的对称轴，点B为抛物线的顶点，

∴n+1= ，

∴n= ﹣1．

∴a为大于2的偶数，存在n，使△ABC是以AC为底边的等腰三角形，n= ﹣1．

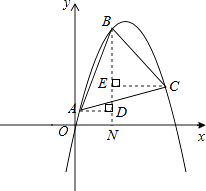
【解析】（1）将点A和点B的坐标代入二次函数的解析式，利用y1=y2得到用n表示a的式子，即可得到答案；（2）将a=11代入解析式后，由题意列出不等式组，求得此不等式组的正整数解；（3）本问为存在型问题．如解答图所示，可以由三角形全等及等腰三角形的性质，判定点B为抛物线的顶点，点A、C关于对称轴对称．于是得到n+1= ，从而可以求出n= ﹣1．
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识，掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点，以及对二次函数的性质的理解，了解增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．