Question

【题目】对于两个相似三角形，如果沿周界按对应点顺序环绕的方向相同，那么称这两个三角形互为顺相似；如果沿周界按对应点顺序环绕的方向相反，那么称这两个三角形互为逆相似．例如，如图①，△ABC∽△A′B′C′，且沿周界ABCA与A′B′C′A′环绕的方向相同，因此△ACB和△A′B′C′互为顺相似；如图②，△ABC∽△A′B′C′，且沿周界ABCA与A′B′C′A′环绕的方向相反，因此△ACB和△A′B′C′互为逆相似．

（1）根据图Ⅰ，图Ⅱ和图Ⅲ满足的条件．可得下列三对相似三角形：①△ADE与△ABC；②△GHO与△KFO；③△NQP与△NMQ；其中，互为顺相似的是；互为逆相似的是 ． （填写所有符合要求的序号）．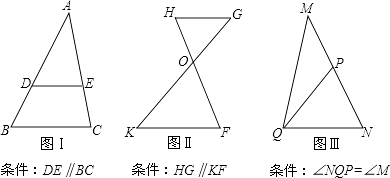

（2）如图③，在锐角△ABC中，∠A＜∠B＜∠C，点P在△ABC的边上（不与点A，B，C重合）．过点P画直线截△ABC，使截得的一个三角形与△ABC互为逆相似．请根据点P的不同位置，探索过点P的截线的情形，画出图形并说明截线满足的条件，不必说明理由．

Answer 1

【答案】
（1）①②；③
（2）

解：根据点P在△ABC边上的位置分为以下三种情况：

第一种情况：如图①，点P在BC（不含点B、C）上，过点P只能画出2条截线PQ1、PQ2，分别使∠CPQ1=∠A，∠BPQ2=∠A，此时△PQ1C、△PBQ2都与△ABC互为逆相似．

第二种情况：如图②，点P在AC（不含点A、C）上，过点B作∠CBM=∠A，BM交AC于点M．

当点P在AM（不含点M）上时，过点P1只能画出1条截线P1Q，使∠AP1Q=∠ABC，此时△AP1Q与△ABC互为逆相似；

当点P在CM上时，过点P2只能画出2条截线P2Q1、P2Q2，分别使∠AP2Q1=∠ABC，∠CP2Q2=∠ABC，此时△AP2Q1、△Q2P2C都与△ABC互为逆相似．

第三种情况：如图③，点P在AB（不含点A、B）上，过点C作∠BCD=∠A，∠ACE=∠B，CD、CE分别交AB于点D、E．

当点P在AD（不含点D）上时，过点P只能画出1条截线P1Q，使∠AP1Q=∠ACB，此时△AQP1与△ABC互为逆相似；

当点P在DE上时，过点P2只能画出2条截线P2Q1、P2Q2，分别使∠AP2Q1=∠ACB，∠BP2Q2=∠BCA，此时△AQ1P2、△Q2BP2

都与△ABC互为逆相似；

当点P在BE（不含点E）上时，过点P3只能画出1条截线P3Q′，使∠BP3Q′=∠BCA，此时△Q′BP3与△ABC互为逆相似．

【解析】（1）根据互为顺相似和互为逆相似的定义即可作出判断；（2）根据点P在△ABC边上的位置分为三种情况，需要分类讨论，逐一分析求解．
【考点精析】解答此题的关键在于理解相似三角形的性质的相关知识，掌握对应角相等，对应边成比例的两个三角形叫做相似三角形．