题目内容
【题目】如图,AB是⊙O的直径, ![]() =
= ![]() ,AB=2,连接AC.
,AB=2,连接AC. 
(1)求证:∠CAB=45°;
(2)若直线l为⊙O的切线,C是切点,在直线l上取一点D,使BD=AB,BD所在的直线与AC所在的直线相交于点E,连接AD. (Ⅰ)试探究AE与AD之间的是数量关系,并证明你的结论;
(Ⅱ)是否为定值?若是,请求出这个定值;若不是,请说明理由.
【答案】
(1)证明:如图1,连接BC,
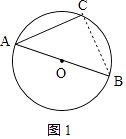
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AC=BC,
∴∠CAB=∠CBA= ![]() =45°;
=45°;
(2)(Ⅰ)解:①当∠ABD为锐角时,如图2所示,作BF⊥l于点F,
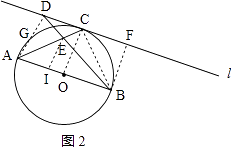
由(1)知△ACB是等腰直角三角形,
∵OA=OB=OC,
∴△BOC为等腰直角三角形,
∵l是⊙O的切线,
∴OC⊥l,
又BF⊥l,
∴四边形OBFC是矩形,
∴AB=2OC=2BF,
∵BD=AB,
∴BD=2BF,
∴∠BDF=30°,
∴∠DBA=30°,∠BDA=∠BAD=75°,
∴∠CBE=∠CBA﹣∠DBA=45°﹣30°=15°,
∴∠DEA=∠CEB=90°﹣∠CBE=75°,
∴∠ADE=∠AED,
∴AD=AE;
②当∠ABD为钝角时,如图3所示,
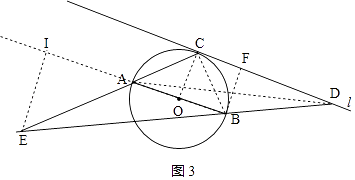
同理可得BF= ![]() BD,即可知∠BDC=30°,
BD,即可知∠BDC=30°,
∵OC⊥AB、OC⊥直线l,
∴AB∥直线l,
∴∠ABD=150°,∠ABE=30°,
∴∠BEC=90°﹣(∠ABE+∠ABC)=90°﹣(30°+45°)=15°,
∵AB=DB,
∴∠ADB= ![]() ∠ABE=15°,
∠ABE=15°,
∴∠BEC=∠ADE,
∴AE=AD;
(Ⅱ)解:①如图2,当D在C左侧时,
由(2)知CD∥AB,∠ACD=∠BAE,∠DAC=∠EBA=30°,
∴△CAD∽△BAE,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴AE= ![]() CD,
CD,
作EI⊥AB于点I,
∵∠CAB=45°、∠ABD=30°,
∴BE=2EI=2× ![]() AE=
AE= ![]() AE=
AE= ![]() ×
× ![]() CD=2CD,
CD=2CD,
∴ ![]() =2;
=2;
②如图3,当点D在点C右侧时,过点E作EI⊥AB于I,
由(2)知∠ADC=∠BEA=15°,
∵AB∥CD,
∴∠EAB=∠ACD,
∴△ACD∽△BAE,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() CD,
CD,
∵BA=BD,∠BAD=∠BDA=15°,
∴∠IBE=30°,
∴BE=2EI=2× ![]() AE=
AE= ![]() AE=
AE= ![]() ×
× ![]() CD=2CD,
CD=2CD,
∴ ![]() =2.
=2.
【解析】(1)由AB是⊙O的直径知∠ACB=90°,由 ![]() =
= ![]() 即AC=BC可得答案;(2)(Ⅰ)分∠ABD为锐角和钝角两种情况,①作BF⊥l于点F,证四边形OBFC是矩形可得AB=2OC=2BF,结合BD=AB知∠BDF=30°,再求出∠BDA和∠DEA度数可得;②同理BF=
即AC=BC可得答案;(2)(Ⅰ)分∠ABD为锐角和钝角两种情况,①作BF⊥l于点F,证四边形OBFC是矩形可得AB=2OC=2BF,结合BD=AB知∠BDF=30°,再求出∠BDA和∠DEA度数可得;②同理BF= ![]() BD,即可知∠BDC=30°,分别求出∠BEC、∠ADB即可得;(Ⅱ)分D在C左侧和点D在点C右侧两种情况,作EI⊥AB,证△CAD∽△BAE得
BD,即可知∠BDC=30°,分别求出∠BEC、∠ADB即可得;(Ⅱ)分D在C左侧和点D在点C右侧两种情况,作EI⊥AB,证△CAD∽△BAE得 ![]() =
= ![]() =
= ![]() ,即AE=
,即AE= ![]() CD,结合EI=
CD,结合EI= ![]() BE、EI=
BE、EI= ![]() AE,可得BE=2EI=2×
AE,可得BE=2EI=2× ![]() AE=
AE= ![]() AE=
AE= ![]() ×
× ![]() CD=2CD,从而得出结论.
CD=2CD,从而得出结论.

【题目】如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则正方形MNPQ与正方形AEFG的面积之比等于。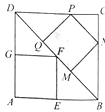
【题目】对一批衬衣进行抽检,统计合格衬衣的件数,得到如下的频数表:
抽查件数(件) | 100 | 150 | 200 | 500 | 800 | 1000 |
合格频数 | 85 | 141 | 176 | 445 | 724 | 900 |
根据表中数据,下列说法错误的是( )
A.抽取100件的合格频数是85
B.任抽取一件衬衣是合格品的概率是0.8
C.抽取200件的合格频率是0.88
D.出售1200件衬衣,次品大约有120件