题目内容
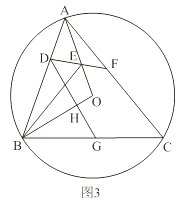
【题目】如图,在△ABC中,分别作其内角∠ACB与外角∠DAC的角平分线,且两条角平分线所在的直线交于点E
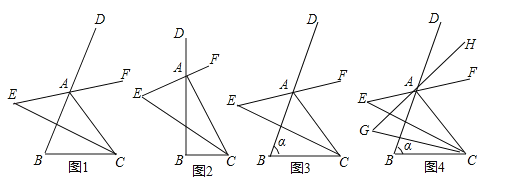
(1)填空:①如图1,若∠B=60°,则∠E= ;
②如图2,若∠B=90°,则∠E= ;
(2)如图3,若∠B=α,求∠E的度数;
(3)如图4,仿照(2)中的方法,在(2)的条件下分别作∠EAB与∠ECB的角平分线,且两条角平分线交于点G,求∠G的度数.
【答案】(1)①30°;②45°;(2)∠E=![]() α;(3)∠G =
α;(3)∠G =![]() α.
α.
【解析】
(1)①根据三角形的外角性质可得∠DAC﹣∠ACB=∠B=60°,再根据角平分线的定义可得∠FAC﹣∠ACE=30°,可求∠E的度数;
②根据三角形的外角性质可得∠DAC﹣∠ACB=∠B=90°,再根据角平分线的定义可得∠FAC﹣∠ACE=45°,可求∠E的度数;
(2)根据三角形的外角性质可得∠DAC﹣∠ACB=∠B=![]() α,再根据角平分线的定义可得∠FAC﹣∠ACE=
α,再根据角平分线的定义可得∠FAC﹣∠ACE=![]() α,可求∠E的度数;
α,可求∠E的度数;
(3)根据角平分线的定和义可得三角形的外角性质可得∠G=∠HAC﹣∠ACG=![]() ∠FAC﹣
∠FAC﹣![]() ∠ACE=
∠ACE=![]() (∠FAC﹣∠ACE),可求∠G的度数.
(∠FAC﹣∠ACE),可求∠G的度数.
(1)①∠DAC﹣∠ACB=∠B=60°.
∵EA平分∠DAC,EC平分∠ACB,∴∠FAC=![]() ∠DAC,∠ACE=
∠DAC,∠ACE=![]() ∠ACB,∴∠E=∠FAC﹣∠ACE=
∠ACB,∴∠E=∠FAC﹣∠ACE=![]() ∠B=30°;
∠B=30°;
②∠DAC﹣∠ACB=∠B=60°.
∵EA平分∠DAC,EC平分∠ACB,∴∠FAC=![]() ∠DAC,∠ACE=
∠DAC,∠ACE=![]() ∠ACB,∴∠E=∠FAC﹣∠ACE=
∠ACB,∴∠E=∠FAC﹣∠ACE=![]() ∠B=45°;
∠B=45°;
(2)∠DAC﹣∠ACB=∠B=α.
∵EA平分∠DAC,EC平分∠ACB,∴∠FAC=![]() ∠DAC,∠ACE=
∠DAC,∠ACE=![]() ∠ACB,∴∠E=∠FAC﹣∠ACE=
∠ACB,∴∠E=∠FAC﹣∠ACE=![]() ∠B=
∠B=![]() α;
α;
(3)∵AG,CG分别是∠EAB与∠ECB的角平分线,∴∠G=∠HAC﹣∠ACG=![]() ∠FAC﹣
∠FAC﹣![]() ∠ACE=
∠ACE=![]() (∠FAC﹣∠ACE)=
(∠FAC﹣∠ACE)=![]() ×
×![]() ∠B=
∠B=![]() α.
α.

 阅读快车系列答案
阅读快车系列答案【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备![]() 现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格 | a | b |
处理污水量 | 240 | 200 |
![]() 求a,b的值;
求a,b的值;
![]() 治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
![]() 在
在![]() 的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.