题目内容
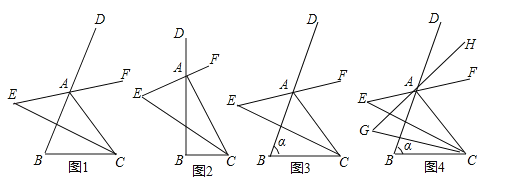
【题目】如图,△ABC和△ADC都是边长相等的等边三角形,点E、F同时分别从点B、A出发,各自沿BA、AD方向运动到点A、D停止,运动的速度相同,连接EC、FC.
(1)在点E、F运动过程中∠ECF的大小是否随之变化?请说明理由;
(2)在点E、F运动过程中,以点A、E、C、F为顶点的四边形的面积变化了吗?请说明理由;
(3)连接EF,在图中找出和∠ACE相等的所有角,并说明理由.

【答案】(1)∠ECF不变为60°.理由见解析;(2)不变化.理由见解析;(3)∠ACE=∠FCD=∠AFE.理由见解析.
【解析】
(1)根据SAS证明△BCE≌△ACF,得到∠ECB=∠FCA,从而证明结论;
(2)结合(1)中证明的全等三角形,即可发现以点A、E、C、F为顶点的四边形的面积即为△ABC的面积;
(3)根据等边三角形的判定可以证明△ECF是等边三角形,再进一步根据平角定义,得到∠AFE+∠DFC=120°,则∠AFE=∠FCD,从而求解.
解:(1)∠ECF不变为60°.
理由如下:
∵△ABC和△ADC都是边长相等的等边三角形,
∴BC=AC=CD,∠B=∠DAC=60°,
又∵E、F两点运动时间、速度相等,
∴BE=AF,
∴△BCE≌△ACF(SAS),
∴∠ECB=∠FCA.
所以∠ECF=∠FCA+∠ACE=∠ECB+∠ACE=∠BCA=60°;
(2)不变化.理由如下:
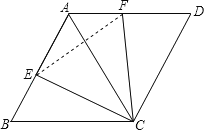
∵四边形AECF的面积=△AFC的面积+△AEC的面积,△BCE≌△ACF,
∴△AEC的面积+△BEC的面积=△ABC的面积;
(3)证明:由(1)知CE=CF,∠ECF=60°,
∴△CEF为等边三角形,
∵∠FCD+∠DFC=120°,∠AFE+∠DFC=120°,
∴∠ECF-∠ACF=∠ACD-∠ACF,即∠AFE=∠FCD,
所以∠ACE=∠FCD=∠AFE.

【题目】某校为了调查学生书写汉字的能力,从八年级800名学生中随机抽选了50名学生参加测试,这50名学生同时听写50个常用汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出不完整的频数分布表和频数分布直方图如图表:
频数分布表
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 8 |
第3组 | 35≤x<40 | 16 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,请你估计该校八年级汉字书写优秀的人数?
(4)第一组中的A、B、C、D 四名同学为提高汉字书写能力,分成两组,每组两人进行对抗练习,请用列表法或画树状图的方法,求A与B名同学能分在同一组的概率.

【题目】某公司招聘人才,对应聘者分别进行阅读能力、专业知识、表达能力三项测试,并将三项测试得分按3:5:2的比例确定每人的最终成绩,现欲从甲乙两选手中录取一人,已知两人的各项测试得分如下表(单位:分)
阅读 | 专业 | 表达 | |
甲 | 93 | 86 | 73 |
乙 | 95 | 81 | 79 |
①请通过相关的计算说明谁将被录用?
②请对落选者今后的应聘提些合理的建议.