题目内容
【题目】有两个内角分别是它们对角的一半的四边形叫做半对角四边形.
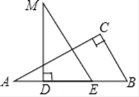
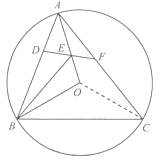
(1)如图1,在半对角四边形ABCD中,∠B=![]() ∠D,∠C=
∠D,∠C=![]() ∠A,求∠B与∠C的度数之和;
∠A,求∠B与∠C的度数之和;

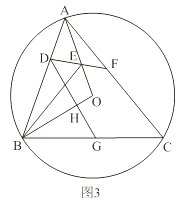
(2)如图2,锐角△ABC内接于⊙O,若边AB上存在一点D,使得BD=BO.∠OBA的平分线交OA于点E,连结DE并延长交AC于点F,∠AFE=2∠EAF.

求证:四边形DBCF是半对角四边形;
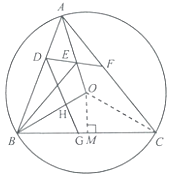
(3)如图3,在(2)的条件下,过点D作DG⊥OB于点H,交BC于点G.当DH=BG时,求△BGH与△ABC的面积之比.
【答案】(1)∠B与∠C的度数之和120°;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)在半对角四边形ABCD中,∠B=![]() ∠D,∠C=
∠D,∠C=![]() ∠A;根据四边形的内角和为360°,得出∠B与∠C的度数之和;
∠A;根据四边形的内角和为360°,得出∠B与∠C的度数之和;
(2)如图连接OC,根据条件先证△BED≌△BEO,再根据全等三角形的性质得出∠BCF=![]() ∠BOE=
∠BOE=![]() ∠BDE;设∠EAF=α,则∠AFE=2∠EAF=2α得出∠EFC=180°-∠AFE=180°-2α;再根据OA=OC得出∠OAC=∠OCA=α, 根据三角形内角和得出∠AOC=180°-∠OAC-∠OCA=180°-2α;从而得证.
∠BDE;设∠EAF=α,则∠AFE=2∠EAF=2α得出∠EFC=180°-∠AFE=180°-2α;再根据OA=OC得出∠OAC=∠OCA=α, 根据三角形内角和得出∠AOC=180°-∠OAC-∠OCA=180°-2α;从而得证.
(3)如图,过点作OM⊥BC于点M,由四边形DBCF是半对角四边形,得出∠ABC+∠ACB=120°,∠BAC=60°,∠BOC=2∠BAC=120°;再由OB=OC,得出∠OBC=∠OCB=30°,BC=2BM=![]() BO=
BO=![]() BD;根据△DBG~△CBA得出答案.
BD;根据△DBG~△CBA得出答案.
试题解析:(1)在半对角四边形ABCD中,∠B=![]() ∠D,∠C=
∠D,∠C=![]() ∠A,
∠A,
∵∠A+∠B+∠C+∠D=360°,
∴3∠B+3∠C=360°,
∴∠B+∠C=120°,
即∠B与∠C的度数之和120°;
(2)在△BED和△BEO中,
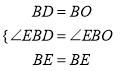 ,
,
∴△BED≌△BEO(SAS),
∴∠BDE=∠BOE,
又∵∠BCF=![]() ∠BOE,
∠BOE,
∴∠BCF=![]() ∠BDE,
∠BDE,
如图,连结OC,
设∠EAF=α,.则∠AFE=2∠EAF=2α,
∴∠EFC=180°-∠AFE=180°-2α,
∵OA=OC,
∴∠OAC=∠OCA=α,
∴∠AOC=180°-∠OAC-∠OCA=180°-2α,
∴∠ABC=![]() ∠AOC=
∠AOC=![]() ∠EFC.
∠EFC.
∴四边形DBCF是半对角四边形;
(3)如图,作过点OM⊥BC于点M.
∵四边形DBCF是半对角四边形,
∴∠ABC+∠ACB=120°,
∴∠BAC=60°,
∴∠BOC=2∠BAC=120°,
∵OB=OC,
∴∠OBC=∠OCB=30°,
∴BC=2BM=![]() BO=
BO=![]() BD,
BD,
∵DG⊥OB,
∴∠HGB=∠BAC=60°,
∵∠DBG=∠CBA,
∴△DBG∽△CBA,
∴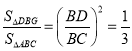 ,
,
∵DH=BG,BG=2HG,
∴DG=3HG,
∴![]() ,
,
∴![]() .
.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案