题目内容
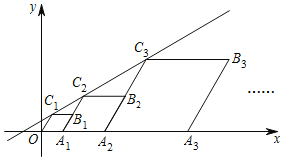
【题目】如图，在平面直角坐标系中，四边形OA1B1C1，A1A2B2C2，A2A3B3C3，…都是菱形，点A1，A2，A3，…都在x轴上，点C1，C2，C3，…都在直线y＝
x+上，且∠C1OA1＝∠C2A1A2＝∠C3A2A3＝…＝60°，OA1＝1，则点C6的坐标是__．
【答案】（47，
）
【解析】
根据菱形的边长求得A1、A2、A3…的坐标然后分别表示出C1、C2、C3…的坐标找出规律进而求得C6的坐标．
解：∵OA1=1，
∴OC1=1，
∴∠C1OA1＝∠C2A1A2＝∠C3A2A3＝…＝60°，
∴C1的纵坐标为：sim60°. OC1＝
，横坐标为cos60°. OC1＝
，
∴C1
，
∵四边形OA1B1C1，A1A2B2C2，A2A3B3C3，…都是菱形，
∴A1C2=2，A2C3=4，A3C4=8，…
∴C2的纵坐标为：sin60°A1C2=
，代入y求得横坐标为2，
∴C2（2，），
∴C3的纵坐标为：sin60°A2C3=
，代入y求得横坐标为5，
∴C3（5，），
∴C4（11，
），C5（23，
），
∴C6（47，）；
故答案为（47，）．
练习册系列答案
相关题目
