题目内容
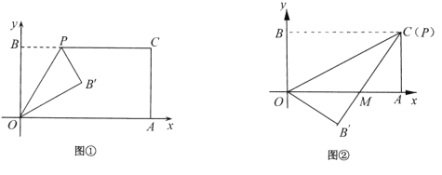
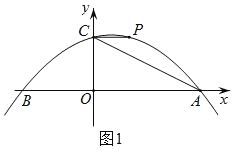
【题目】如图1,在平面直角坐标系中,抛物线y=![]() x2+
x2+![]() x+3与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,过点C作x轴的平行线交抛物线于点P.连接AC.
x+3与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,过点C作x轴的平行线交抛物线于点P.连接AC.
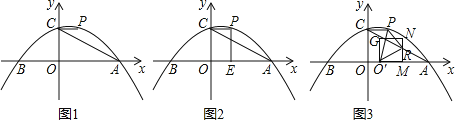
(1)求点P的坐标及直线AC的解析式;
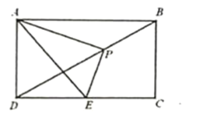
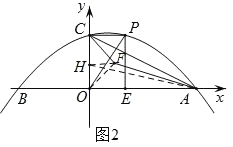
(2)如图2,过点P作x轴的垂线,垂足为E,将线段OE绕点O逆时针旋转得到OF,旋转角为α(0°<α<90°),连接FA、FC.求AF+![]() CF的最小值;
CF的最小值;
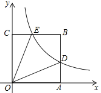
(3)如图3,点M为线段OA上一点,以OM为边在第一象限内作正方形OMNG,当正方形OMNG的顶点N恰好落在线段AC上时,将正方形OMNG沿x轴向右平移,记平移中的正方形OMNG为正方形O′MNG,当点M与点A重合时停止平移.设平移的距离为t,正方形O′MNG的边MN与AC交于点R,连接O′P、O′R、PR,是否存在t的值,使△O′PR为直角三角形?若存在,求出t的值;若不存在,请说明理由.
【答案】(1)P(2,3),yAC=﹣![]() x+3;(2)
x+3;(2)![]() ;(3)存在,t的值为
;(3)存在,t的值为![]() ﹣3或
﹣3或![]() ,理由见解析
,理由见解析
【解析】
(1)由抛物线y=![]() x2+
x2+![]() x+3可求出点C,P,A的坐标,再用待定系数法,可求出直线AC的解析式;
x+3可求出点C,P,A的坐标,再用待定系数法,可求出直线AC的解析式;
(2)在OC上取点H(0,![]() ),连接HF,AH,求出AH的长度,证△HOF∽△FOC,推出HF=
),连接HF,AH,求出AH的长度,证△HOF∽△FOC,推出HF=![]() CF,由AF+
CF,由AF+![]() CF=AF+HF≥AH,即可求解;
CF=AF+HF≥AH,即可求解;
(3)先求出正方形的边长,通过△ARM∽△ACO将相关线段用含t的代数式表示出来,再分三种情况进行讨论:当∠O'RP=90°时,当∠PO'R=90°时,当∠O'PR=90°时,分别构造相似三角形,即可求出t的值,其中第三种情况不存在,舍去.
(1)在抛物线y=![]() x2+
x2+![]() x+3中,
x+3中,
当x=0时,y=3,
∴C(0,3),
当y=3时,x1=0,x2=2,
∴P(2,3),
当y=0时,则![]() x2+
x2+![]() x+3=0,
x+3=0,
解得:x1=﹣4,x2=6,
B(﹣4,0),A(6,0),
设直线AC的解析式为y=kx+3,
将A(6,0)代入,
得,k=﹣![]() ,
,
∴y=﹣![]() x+3,
x+3,
∴点P坐标为P(2,3),直线AC的解析式为y=﹣![]() x+3;
x+3;
(2)在OC上取点H(0,![]() ),连接HF,AH,
),连接HF,AH,
则OH=![]() ,AH=
,AH=![]() ,
,
∵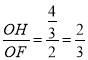 ,
,![]() ,且∠HOF=∠FOC,
,且∠HOF=∠FOC,
∴△HOF∽△FOC,
∴![]() ,
,
∴HF=![]() CF,
CF,
∴AF+![]() CF=AF+HF≥AH=
CF=AF+HF≥AH=![]() ,
,
∴AF+![]() CF的最小值为
CF的最小值为![]() ;
;
(3)∵正方形OMNG的顶点N恰好落在线段AC上,
∴GN=MN,
∴设N(a,a),
将点N代入直线AC解析式,
得,a=﹣![]() a+3,
a+3,
∴a=2,
∴正方形OMNG的边长是2,
∵平移的距离为t,
∴平移后OM的长为t+2,
∴AM=6﹣(t+2)=4﹣t,
∵RM∥OC,
∴△ARM∽△ACO,
∴![]() ,
,
即![]() ,
,
∴RM=2﹣![]() t,
t,
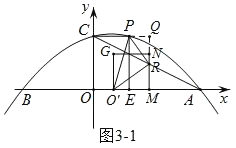
如图3﹣1,当∠O'RP=90°时,延长RN交CP的延长线于Q,
∵∠PRQ+∠O'RM=90°,∠RO'M+∠O'RM=90°,
∴∠PRQ=∠RO'M,
又∵∠Q=∠O'MR=90°,
∴△PQR∽△RMO',
∴![]() ,
,
∵PQ=2+t-2=t,QR=3﹣RM=1+![]() t,
t,
∴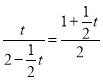 ,
,
解得,t1=﹣3﹣![]() (舍去),t2=
(舍去),t2=![]() ﹣3;
﹣3;
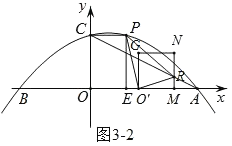
如图3﹣2,当∠PO'R=90°时,
∵∠PO'E+∠RO'M=90°,∠PO'E+∠EPO'=90°,
∴∠RO'M=∠EPO',
又∵∠PEO'=∠O'MR=90°,
∴△PEO'∽△O'MR,
∴![]() ,
,
即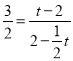 ,
,
解得,t=![]() ;
;
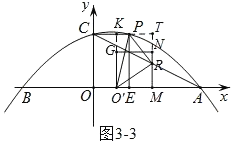
如图3﹣3,当∠O'PR=90°时,延长O’G交CP于K,延长MN交CP的延长线于点T,
∵∠KPO'+∠TPR=90°,∠KO'P+∠KPO'=90°,
∴∠KO'P=∠TPR,
又∵∠O'KP=∠T=90°,
∴△KO'P∽△TPR,
∴![]() ,
,
即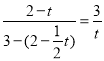 ,
,
整理,得t2-![]() t+3=0,
t+3=0,
∵△=b2﹣4ac=﹣![]() <0,
<0,
∴此方程无解,故不存在∠O'PR=90°的情况;
综上所述,△O′PR为直角三角形时,t的值为![]() ﹣3或
﹣3或![]() .
.

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案