题目内容
【题目】某养殖场计划用96米的竹篱笆围成如图所示的①、②、③三个养殖区域,其中区域①是正方形,区域②和③是矩形,且AG∶BG=3∶2.设BG的长为2x米.
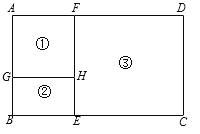
(1)用含x的代数式表示DF= ;
(2)x为何值时,区域③的面积为180平方米;
(3)x为何值时,区域③的面积最大?最大面积是多少?
【答案】(1)48-12x;(2)x为1或3;(3)x为2时,区域③的面积最大,为240平方米
【解析】
(1)将DF、EC以外的线段用x表示出来,再用96减去所有线段的长再除以2可得DF的长度;
(2)将区域③图形的面积用关于x的代数式表示出来,并令其值为180,求出方程的解即可;
(3)令区域③的面积为S,得出x关于S的表达式,得到关于S的二次函数,求出二次函数在x取值范围内的最大值即可.
(1)48-12x
(2)根据题意,得5x(48-12x)=180,
解得x1=1,x2=3
答:x为1或3时,区域③的面积为180平方米
(3)设区域③的面积为S,则S=5x(48-12x)=-60x2+240x=-60(x-2)2+240
∵-60<0,∴当x=2时,S有最大值,最大值为240
答:x为2时,区域③的面积最大,为240平方米

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案【题目】某水产养殖户进行小龙虾养殖. 已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,日销售量![]() 与时间第
与时间第![]() 天之间的函数关系式为
天之间的函数关系式为![]() (
(![]() ,
,![]() 为整数),销售单价
为整数),销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间满足一次函数关系如下表:
天之间满足一次函数关系如下表:
时间第 | 1 | 2 | 3 | … | 80 |
销售单价 | 49. 5 | 49 | 48. 5 | … | 10 |
(1)写出销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间的函数关系式;
天之间的函数关系式;
(2)在整个销售旺季的80天里,哪一天的日销售利润最大?最大利润是多少?
【题目】某大学生创业团队有研发、管理和操作三个小组,各组的日工资和人数如下表所示.现从管理组分别抽调1人到研发组和操作组,调整后与调整前相比,下列说法中不正确的是( )
操作组 | 管理组 | 研发组 | |
日工资(元/人) | 260 | 280 | 300 |
人数(人) | 4 | 4 | 4 |
A.团队平均日工资不变B.团队日工资的方差不变
C.团队日工资的中位数不变D.团队日工资的极差不变