题目内容
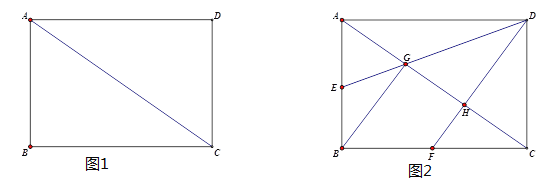
【题目】如图,在矩形ABCD中,AB=3,BC=6,若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为( )

A. 1B. ![]() C. 2D. 4
C. 2D. 4
【答案】C
【解析】
如图,延长FH交AB于点M,由BE=2AE,DF=2FC,G、H分别是AC的三等分点,证明EG//BC,FH//AD,进而证明△AEG∽△ABC,△CFH∽△CAD,进而证明四边形EHFG为平行四边形,再根据平行四边形的面积公式求解即可.
如图,延长FH交AB于点M,
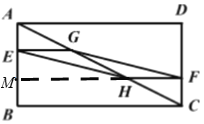
∵BE=2AE,DF=2FC,AB=AE+BE,CD=CF+DF,
∴AE:AB=1:3,CF:CD=1:3,
又∵G、H分别是AC的三等分点,
∴AG:AC=CH:AC=1:3,
∴AE:AB=AG:AC,CF:CD=CH:CA,
∴EG//BC,FH//AD,
∴△AEG∽△ABC,△CFH∽△CDA,BM:AB=CF:CD=1:3,∠EMH=∠B,
∴EG:BC=AE:AB=1:3,HF:AD=CF:CD=1:3,
∵四边形ABCD是矩形,AB=3,BC=6,
∴CD=AB=3,AD=BC=6,∠B=90°,
∴AE=1,EG=2,CF=1,HF=2,BM=1,
∴EM=3-1-1=1,EG=FH,
∴EG![]() FH,
FH,
∴四边形EHFG为平行四边形,
∴S四边形EHFG=2×1=2,
故选C.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目